Ein Polykubus besteht aus mehreren Würfeln, die an Quadratflächen verbunden sind.
Es gibt acht Tetrakuben.
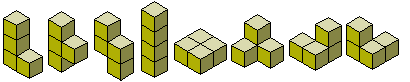
Beachten Sie, dass die ersten fünf Stücke Körperausführungen der Tetrominos sind, während die übrigen drei echt dreidimensional sind. In der Darstellung werden die Polykuben höherer Ordnung, die aus entsprechenden Polyominoes hervorgehen, nicht mehr gezeigt werden. Beachten Sie weiter, dass die beiden letzten Stücke spiegelbildlich sind. Im Gegensatz zu den Polyominoes, für die wir die dritte Dimension haben, um sie zu spiegeln, können wir unsere Polykuben nicht in der vierten Dimension spiegeln. So betrachten wir allgemein Bild und Spiegelbild als verschieden, obwohl wir diese Wahl nicht machen müssen.
Obwohl viele Konstruktionen mit Tetrakuben möglich sind, beschränkt doch die begrenzte Anzahl die Entwurfmöglichkeiten und wenn wir zu den Pentakuben kommen, dann können wir unserer Kreativität freien Lauf lassen.
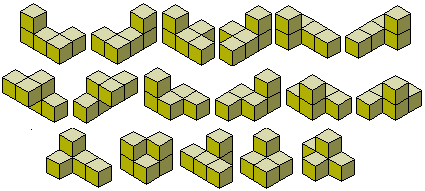
Es gibt 29 Pentakuben, die aus den 12 Pentomino-Körpern bestehen und den 17 anderen Körpern, die unten gezeigt werden.
Unten sind einige Konstruktionen, die mit dem vollen Satz der Pentakuben gebaut werden können.
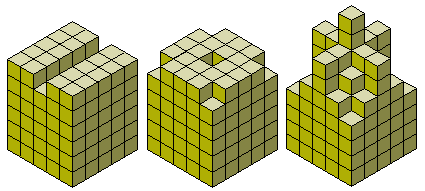
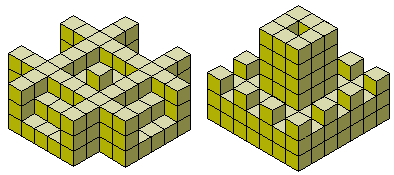
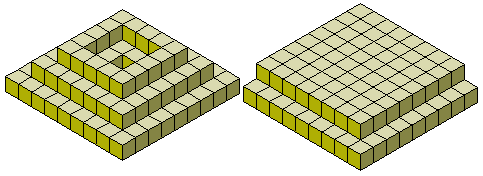
Bruno Gilleta betreibt eine Reihe von Pentakubus-Seiten einschließlich Java Animationen der Quader 3x4x5 und 2x5x6 aus den 12 Pentomino-Körpern. Denjenigen, die an weiteren Konstruktionen mit Pentakuben interessiert sind, sei die Pentakubus-Wettbewerb-Seite empfohlen.
Die Pentakuben sind der erste Satz von Polykuben, bei dem wir weitere Stücke finden können, wenn wir nicht auf drei Dimensionen beschränkt sind. Wenn wir nach vierdimensionalen Pentakuben Ausschau halten, sollten wir Paare von Bild und Spiegelbild weglassen und vier weitere Stücke hinzufügen. Das führt zu 12 ebenen Stücken und die 15 unten. Die vierdimensionalen Stücke haben einen grünen Würfel, bei denen ein Würfel angefügt werden muss in der weiteren Dimension. Beachten Sie, dass es ein vierdimensionales Paar von Bild und Spiegelbild gibt
Es gibt also insgesamt 27 Stücke, die den 3x3x3x5-Hyperquader unten bilden. Beachten Sie, dass wir ein vierdimensionales Paar von Bild und Spiegelbild vor uins haben, und in höheren Dimensionen gibt es nur 26 Stücke.
Es gibt 166 Hexakuben, die aus den Körperversionen der 35 Hexominos bestehen und den folgenden 131 Stücken.

Das Gesamtvolumen der 166 Hexakuben ist 996, und eine Reihe von Quadern kann mit einem vollen Satz hergestellt werden. Da es Stücke gibt, die in zwei senkrecht zueinander liegenden Richtungen 3 Würfel haben, gibt es nur die Quader 2x3x166, 2x6x83 and 3x4x83, die aus einem vollen Satz gebaut werden können. Wenn wir von jedem Spiegelpaar nur eins verwenden, dann bleiben 112 Stücke übrig, die 2x3x112, 2x6x56 and 3x4x56-Quader bilden (siehe Abbildungen).
Unten ist eine andere Konstruktion, die mit allen 166 Stücken gebaut werden können.

Falls Sie sich entschließen, einen Satz selbst herzustellen oder einen Satz bei Kadon zu kaufen (das ist die einzige Stelle - so weit ich weiß - wo er verkauft wird), werden Sie erstaunt sein, wie man eine Konstruktion wie oben zu bauen beginnt: Die beste Weg ist von oben nach unten zu gehen! Wenn man ein Gestell mit der Form als zu füllendes Loch herstellt, nimmt man zuerst die komplizierteren Stücke und kommt in eine Situation, wo man (hoffentlich) nur noch die Hexominos zur Verfügung hat, um die untere Schicht zu legen.Bevor man sich an Kompliziertem versucht, sollte man die Quader, die oben aufgeführt sind, bauen, oder man sollte für einen noch leichteren Start die Hexakuben in einen Würfel der Kantenlänge 10 einpassen und 4 Löcher lassen. Zuerst lasse die Löcher irgendwo sein, aber versuche sie dann in Mustern zu legen wie unten gezeigt oder lege die Löcher an den Rand. Mit etwas Mühe sollte man fähig sein einen 9x10x10-Quader mit 150 Stücken zu bilden und 15 Hexominos übrig zu behalten. Dann kann man eine Reihe verschiedener Muster herstellen ohne zu große Reorganisation.
Es gibt 1023 Heptakuben, und wenn Sie einen Satz sehen wollen, dann, denke ich, sollten Sie ihn selbst herstellen! Ich kenne niemanden, der ihn gezeichnet oder gar gebaut hat. Jedoch sind Konstruktionen über die 108 Heptakuben, die von den Heptominoes abgeleitet werden, untersucht worden. Einzelheiten über die möglichen Quader aus diesem Satz findet man in Mike Reids Zusammenstellungen in Torsten Sillkes Seite, oder sehen Sie sich die Darstellungen der Lösungen der Heptomino-Packungen an. In diesen Zeichnungen bedeutet ein Punkt eine Fortsetzung nach oben, ein Kreis nach unten und ein Punkt im Kreis zeigt eine Fortsetzung in beide Richtungen an.
Oktakuben
Hier soll hier nicht versucht werden die Oktakuben zu untersuchen. Sie sollen nur als Problem genannt werden. Es ist wohlbekannt, dass eine Reihe von Hexominos Netze eines Würfels sind, und in ähnlicher Weise werden einige Oktokuben "Netze" eines Hyperkubus sein. Ein Beispiel wird unten gezeigt und das hier aufgeworfene Problem ist alle Oktokuben zu finden, die Netze eines Hyperkubus sind.