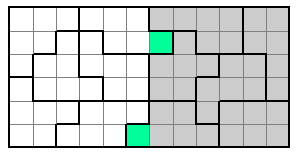
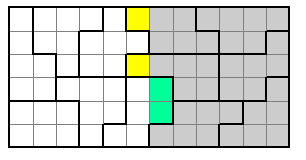
In this second example the two yellow squares must have the same two numbers as the two green squares.
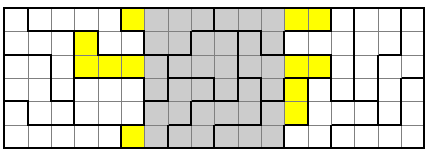
In this example we have six disconnected squares in each of the two outer panels. Each set of yellow sqaures must contain all numbers with no repetition.
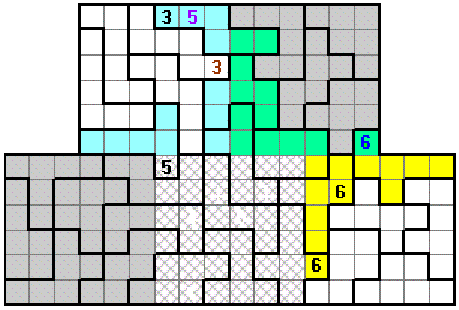
Finally we look at a more complex situation. Firstly in the bottom right panel there are 12 yellow squares which do not belong to complete polyominoes. The 12 numbers here must be two sets of 1 to 6 inclusive and since we already have two 6's this forces the blue 6 as shown.
If we next consider the top left panel 12 blues squares we see that we need two 5's but since these cannot be in the leftmost four squares in the bottom row one must be in the right hand column. Since only one can be there we are forced to conclue that the second 5 must be the purple 5 shown.
Finally since there are two 3's in the blue squares the only place for a 3 in the bottom row is as shown in orange.
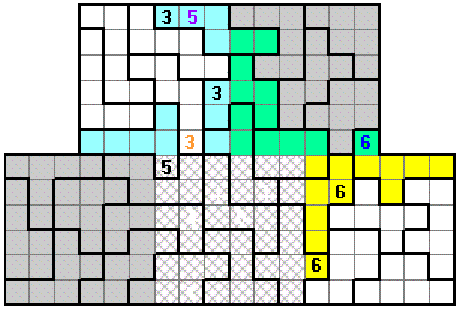
Of course, this is an example only and the above cannot be solved as the blue T-shaped piece cannot now contain a 3. This shows that the only place for a 3 in the right hand column of the top left panel is as shown here in brown..