Other
Sets Based on Polyominoes
The following solutions have been found using Peter Esser's solver which
can be downloaded from http://members.tripod.de/polyforms.
If you find any other interesting solutions using the solver and would like
them included here please send them to me.
Some diagrams contain figures not yet solved.
The definition of a sliced rectangle should be clear from the diagrams.
It is merely a rectangle with a corner sliced off with the type of slice
depending on the type of polyform used. Here we concentrate on single slices
(one corner only) but multiple slices could be considered.


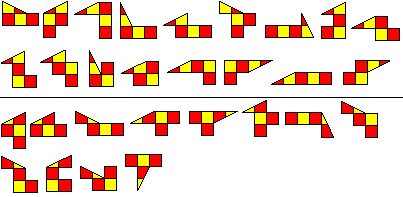
Tromino + half square

Tromino + half domino
If we use one piece twice then a number of rectangles are
possible as well as three or five congruent pieces. The 3x40 rectangle is
by Roel Huisman.
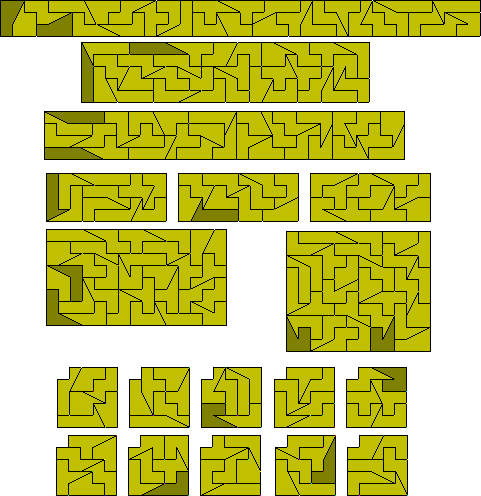
With the full set a number of sliced rectangles can be made.
If we use a chessboard colouring on these pieces then we
see that 17 have a colouring of 2¼ to 1¾ an excess of ½
whereas the remaining 12 pieces have a colouring of 2¾ to 1¼
which gives an excess of 1½ (see below). This will mean that the
piece used twice must be one of the 17 pieces with an excess of ½
using an analysis similar to that for the
domsliced tetrominoes.
As an example here are the remaining 16 solutions for the
5x24 rectangle above.
Monomino + two half squares
Monomino + three half squares
One piece used twice
One sided set
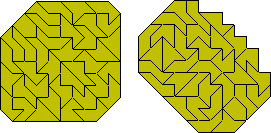

Monomino + four half squares
Three rectangles can be made with one piece left over.
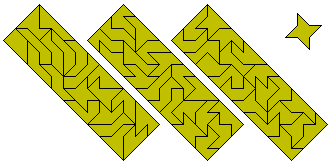
Tetromino - two half squares
The figure at the top left is by Roel Huismann
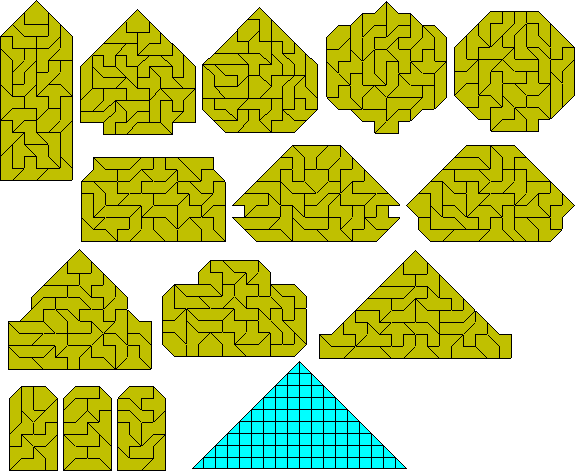
one-sided set
At least one rectangle and two sliced rectangles are possible as well as
a similar hole problem.
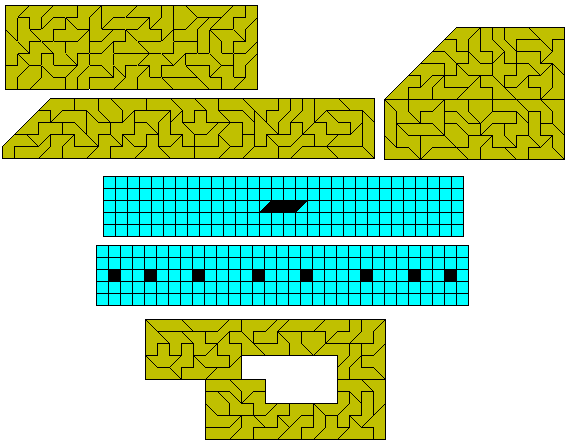

Tetromino + half square
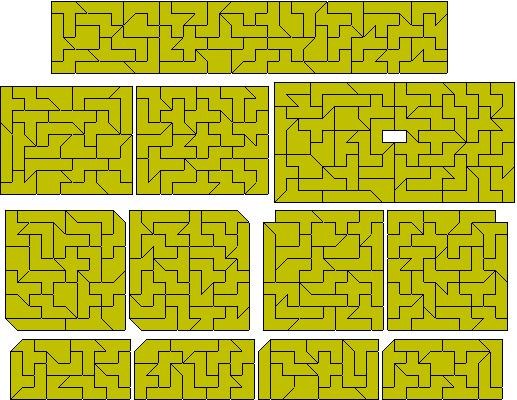
It is also possible to make a number of sliced rectangles
with this set. Notice that one solution can form two different sliced rectangles
depending on whether the rectangle is placed at the side of below the sliced
section.
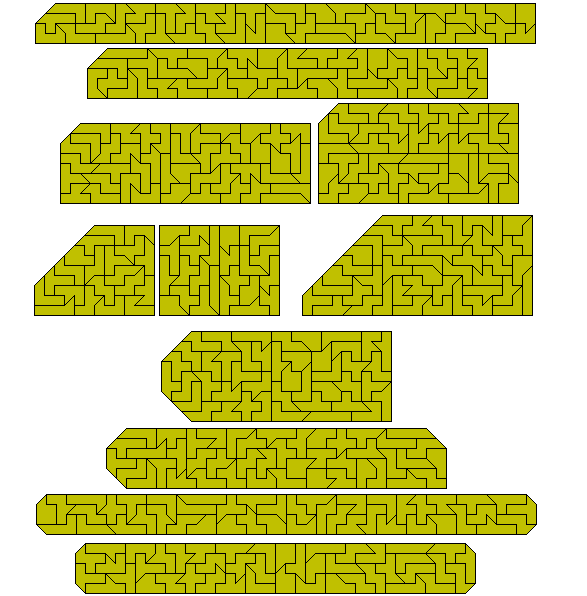

Tromino + half tromino (one pieced used twice)
With just the full set it is possible to make sliced rectangles.

Tromino + two half squares
This set cannot form rectangles or sliced rectangles since any figure formed
must have an excess of 4n+2 squares by colouring.

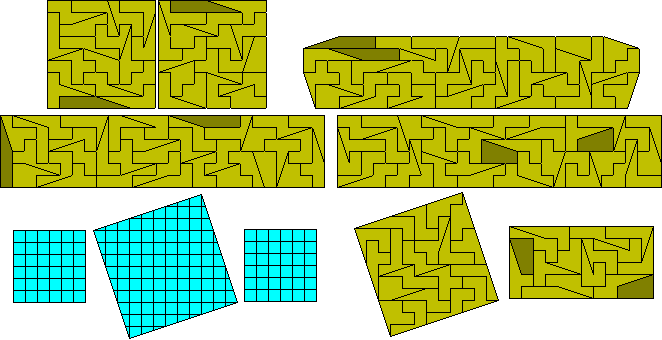
Half tromino + two squares
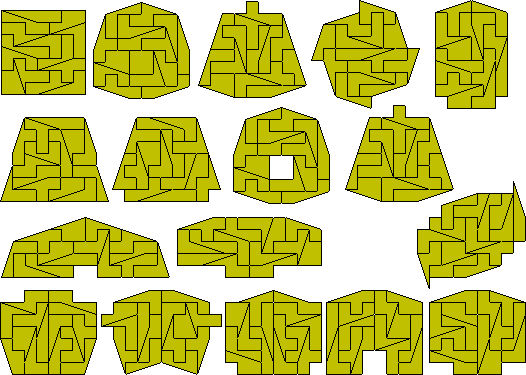
The square at the top left is by Peter Esser. Each figure
in the bottom row is made up of two congruent halves.
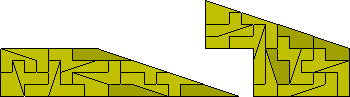
It is also possible to make a fourfold replica of some of the pieces if we
use the replicated piece three times.

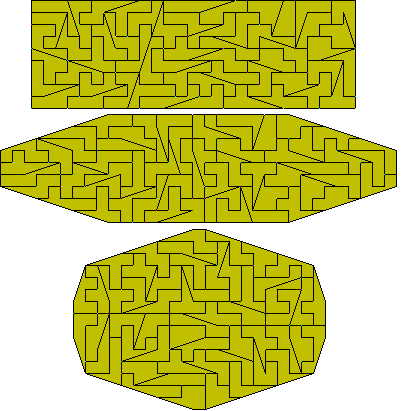
Half tromino + three squares
These constructions are by Peter Esser. Notice that the lower two are made
of two congruent parts.
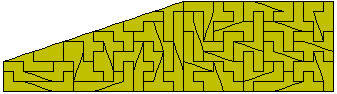
There is just one sliced rectangle which can be made.
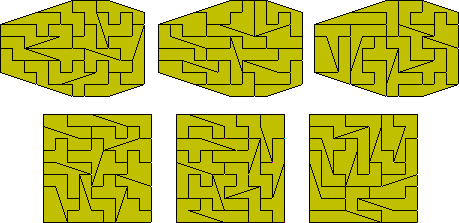
It is also possible, but very difficult, to pack the pieces
into three congruent shapes. Three 9x9 squares have been found by Peter Esser
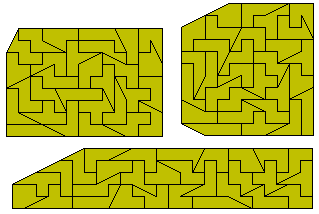
We can also consider a similar set - the tromsliced hexominoes.
The is set can be obtained from the above by removing the two pieces where
removing half a tromino from an hexomino would take away an internal join
between squares. The 6x39 rectangle below was found by Roel Huismann who
also found the two squares made from the set.
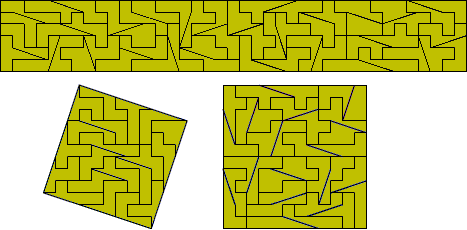

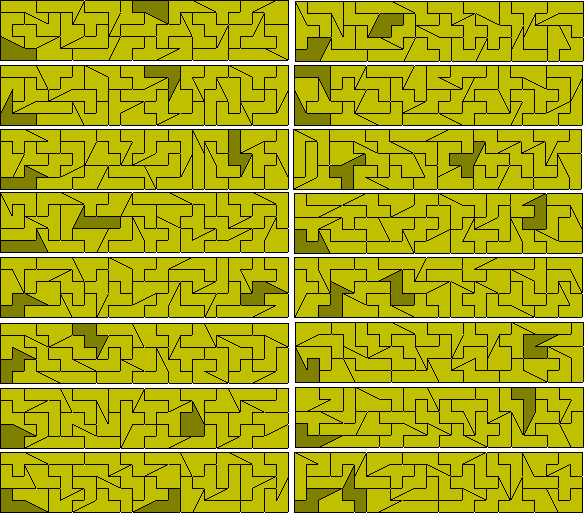
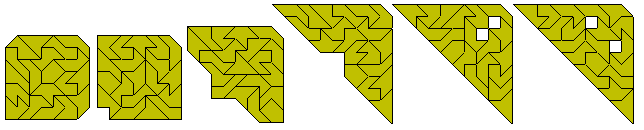
Tetromino Plus Half Tromino
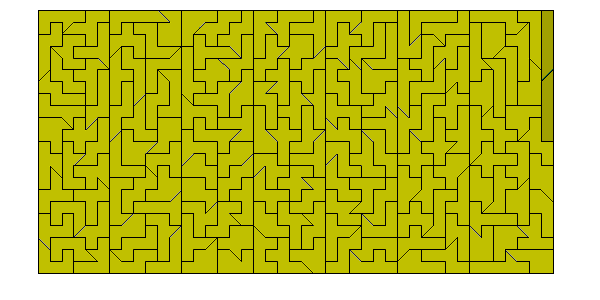
This set consists of 126 pieces with a total area of 693 squares
and can make a number of simultaneous rectangles as shown here (solutions
by Peter Esser). No 3x231 rectangle can be made as there are pieces with width
four in two directions. A number of parallelograms are also possible (solutions
by Peter Esser).
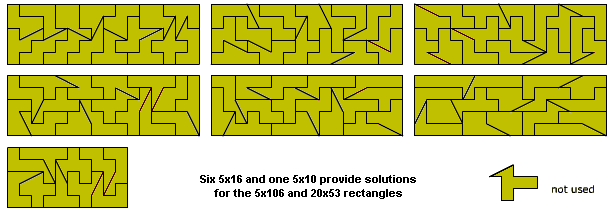
The figure below shows a construction which can make the 7x99
rectangle, parallelogram or trapezium.
It may be possible with this set to remove one piece and then
form five fivefold copies of that piece with the rest of the set. The below
shows one possibility.
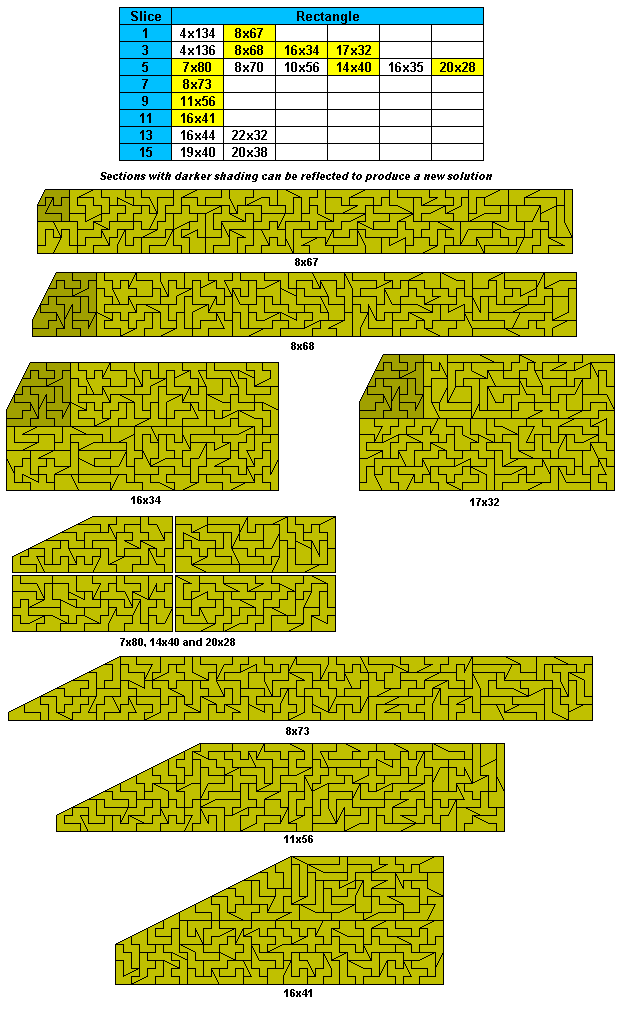
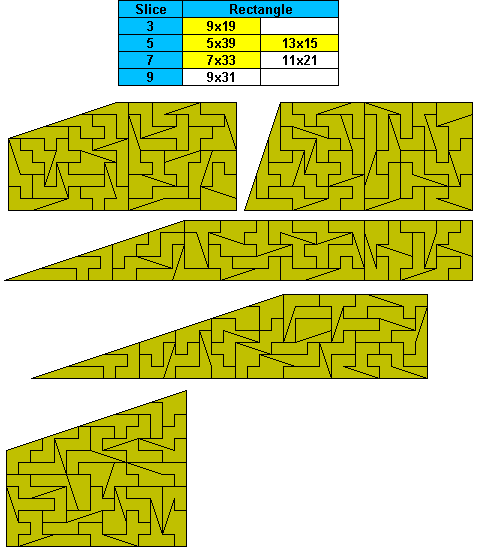
There are also two sliced rectangles which might be possible - 9x83 with
a size 6 slice and a 21x47 with a size 14 slice.

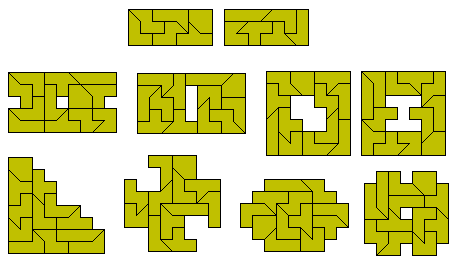
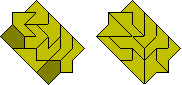
Pentominoes Plus Half Square
This set consists of 172 pieces including on with a hole.
Roel Huisman has constructed the 43x22 rectangle below by omitting the piece
with a hole and using another piece twice.
A number of sliced rectangles is possible with the set if
we omit the piece with a hole.


Tetrominoes Plus Half Domino
This set consists of 107 pieces and Roel Huisman has
constructed the rectangles below by omitting one of the pieces.
A number of sliced rectangles is be possible with the
full set.