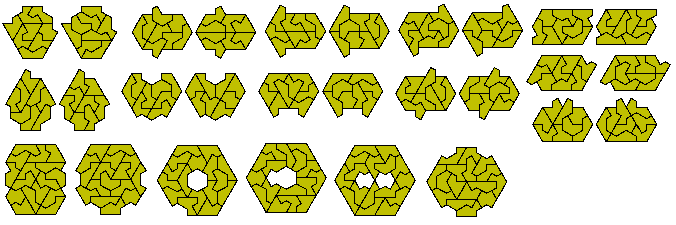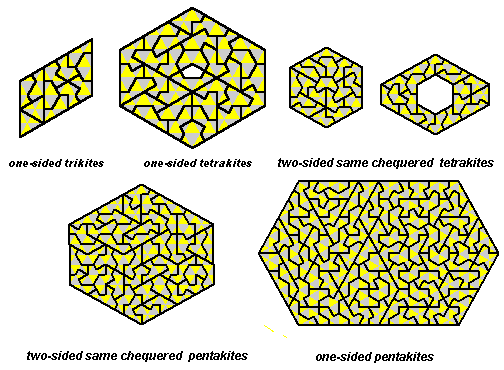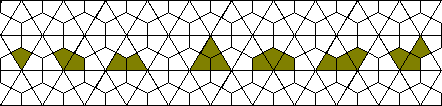
The 14 one-sided tetrakites are shown below. The trepezia are made with one piece used twice.
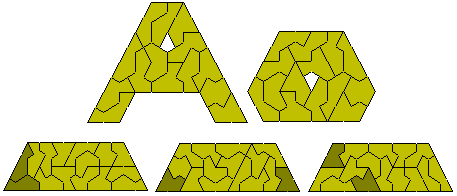
Brendan Owen has produced a number of figures for this set.
Brendan also produced the following trapezium made with the 27 pentakites
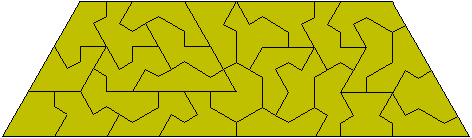
and also found a solution to the following construction.
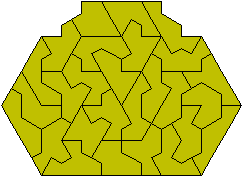
These figures were found using Peter Esser's trisolve program. The trapezium at the top right is the same as Brendan's except that it is divided into a parallelogram and a trapezium (Brendan has gone further and spilt this trapezium into three trapezia). It is possible to make three copies of this smaller trapezium with the set.
The trapezium above is an enlarged model of a pentiamond. Models of the other three can also be made.
Brendan has also made some other pentakite figures based on a hexagon.

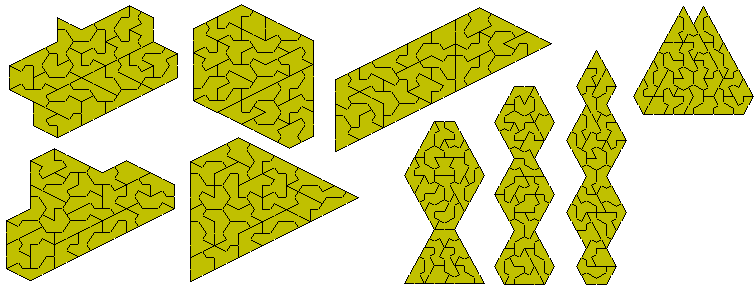
There are 48 one-sided pentakites. This first diagram shows all possible paralleograms and trapezia which can be made with the set..
It is possible to make enlarged copies of each of the pentiamonds with this set.
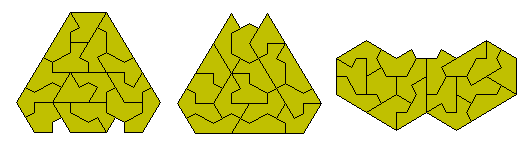
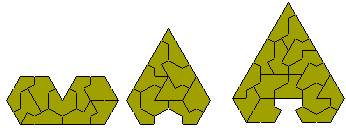
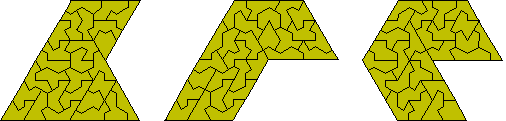
Other symmetric constructions are possible. The figure at the left is an examples of a triangle with a hole in the shape of a trikite. There should be three other such constructions. The costruction at the top right consists of four congruent parts. Brendan Owen has shown that it is impossible to find eight hexagons (half of each of these shapes) but has found the two sets of eight consgruent shapes below.
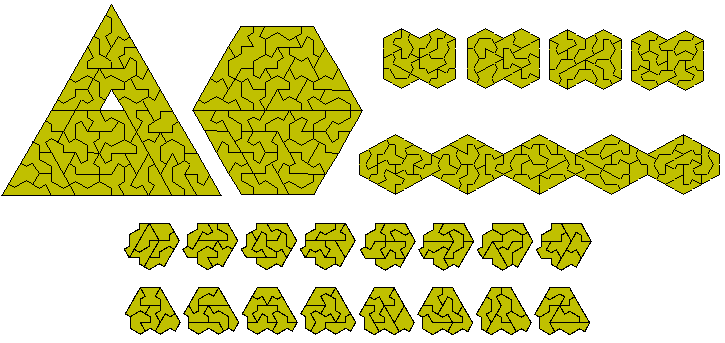
Brendan has also made the figure below made with the 84 hexakites without an internal hole.

Patrick Hamlyn has improved on this by finding a solution made up of seven separate hexagons and has also made the two stars.The first star is made up of six congruent parts.
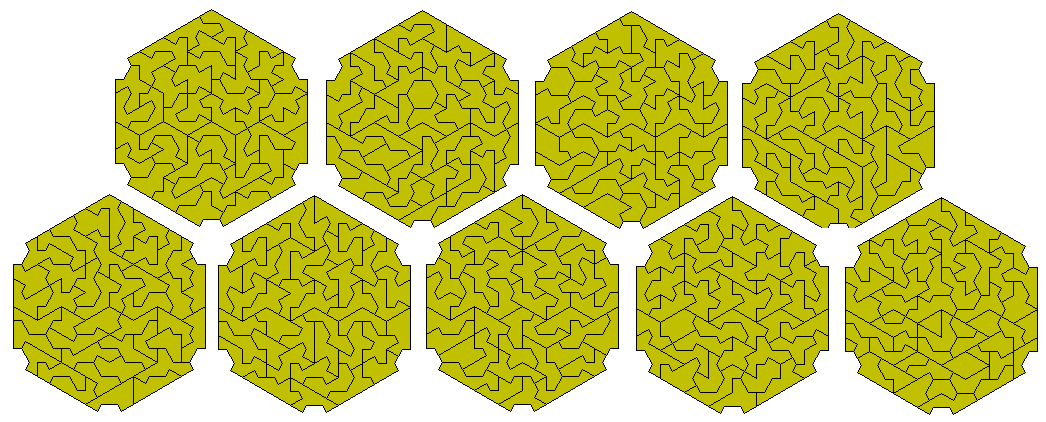
There are 262 heptakites four of which have a hole. The remaining 258 pieces can form six congruent figures as shown below.
This set has 158 pieces with a total area of 948. One piece has a hole but it is very hard to make symmetrical constructions with either set. The figure below shows a construction with 946 of the pieces. The pieces omitted are the one with a hole and the other piece shown in the lower diagram. On a three colour colouring we see that both pieces have two of each colour however while green and blue kites are in opposite directions the two yellow kites are aligned in the same direction. Any design for a full set must take this into consideration.
Working with the above constraints a symmetrical solution with all 158 pieces is possible as shown here. Each solution used the same five sections.
Constructions made combinations of sets.
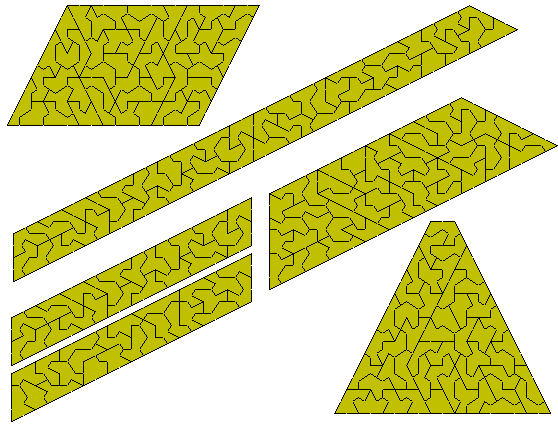
The set consisting of one sided pieces 1 to 4 can make the following construction.
Brendan Owen has packed the set of 44 pieces obtained by combining the kites from one to five into a triangle of side eight. While I do not have this solution but a nuumber of soultions with this set are shown below.
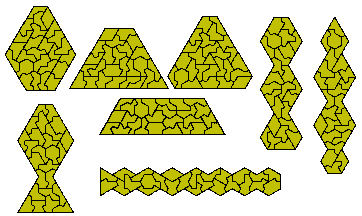
A number of the above construction can be made with one or other of the following where four triangle or four traoezia can be made with the set.
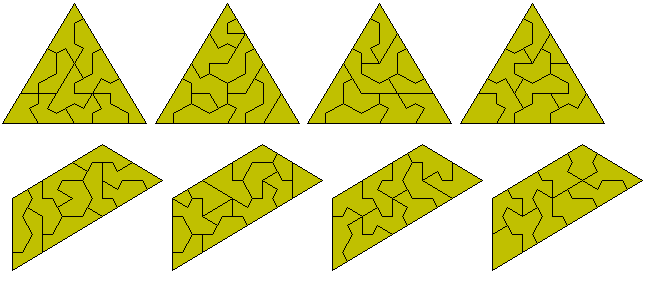
The combined set of one sided polykites size 1 to 5 can make five triangles as shown here
and can also form the hexagon below.
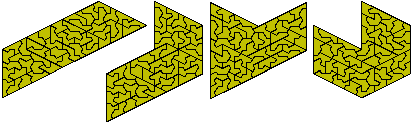
The set formed by combining sizes one to six consists of 129 pieces with a total area of 702. While one of the hexakites has a hole this can be filled by the monokite to produce a number of constructions.Constructions are shown below. The first consists of three hexagons and the next two are made of six congruent sections and the final image is a set of six congruent trapezia.
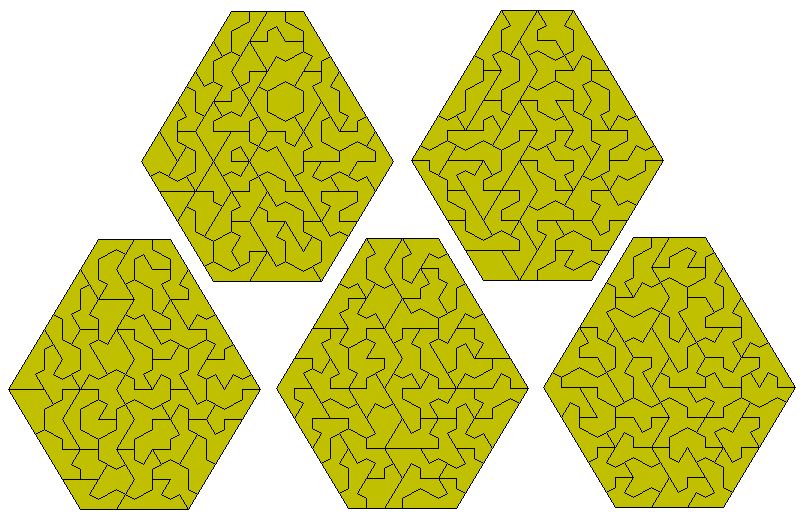
It is also possible to make nine congruent shapes with this set.
This set could form mutiple triangles in a number of ways but the only one in which all triangles are different in size is - 2, 6, 7, 8, 9
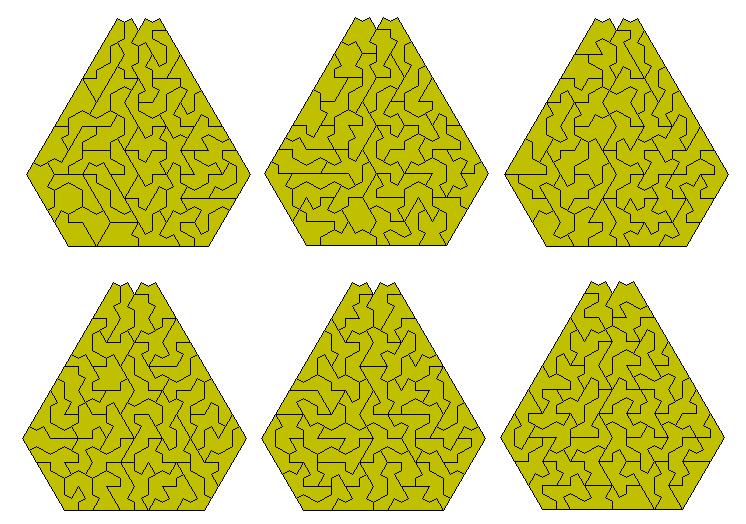
The one sided polykites size 1 to 6 make a set of 231 pieces with a total area of 1275. These are shown blow in a construction consisting of five congruent shapes. It may also be possible to make sets of 15, 17 and 25 congruent shapes.

This set can also make nine or eighteen congruent constructions.
Peter Esser's solver also allows us to find solutions for chequered polykites.
In counting the perimeter of a polykite we can use the length of the longer side of the kite as our unit. On this basis there are nine perimeter 6 pieces with a total area of 39 units and 25 perimeter seven pieces with a total area of 135 units. The first diagram shows two constructions with the perimeter six set and a construction with the 15 pieces one-sided set.