
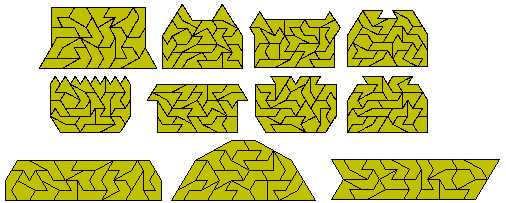
If we remove half a rhombus (by the long diagonal) from the polyiamonds we form rhombsliced polyiamonds. The diagram below shows the three rhombsliced tetriamonds; the seven rhombsliced pentiamonds and the twenty rhombsliced hexiamonds. This last set has a total area of 100 triangles and might have made some interesting figures such as a side 10 triangle or a number of parallelograms. Unfortunately the set has three pieces with an unbalanced colouring (a excess of two triangles each) which means that none of these figures can be made. Brendan Owen has placed 18 of them into a dodecagon as shown below.

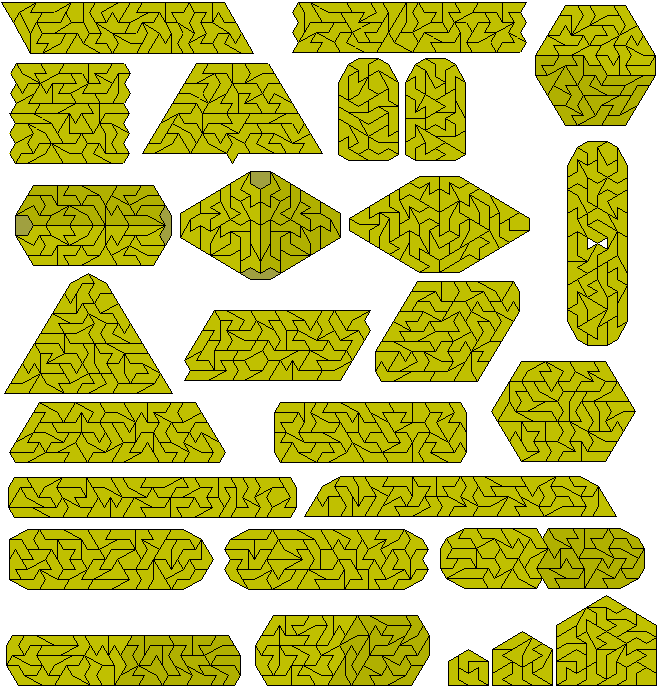
Any figure which might be made with the full set must have a colour excess of 2 or 6. Patrick Hamlyn produced the symmetric figure at the top left which has an excess of two. (This is the same set as we get when adding four triangles to a single rhomb)
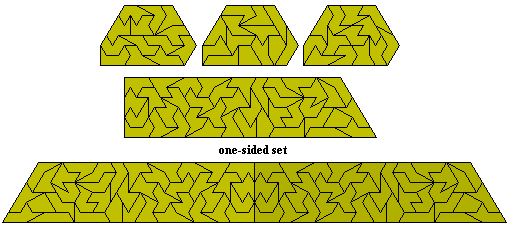
If we look at the one-sided set we get 38 pieces. This parallelogram is also by Patrick.
Constructions with these can be seen on a separate page.
There are 158 rhombsliced octiamonds shown here in a 7x79 parallelogram.This set, as with the rhombsliced hexiamonds, has a number of unbalanced pieces. The number is, however, even and so any figure must be one of area 1100 with an excess colouring of 4n.
![]()
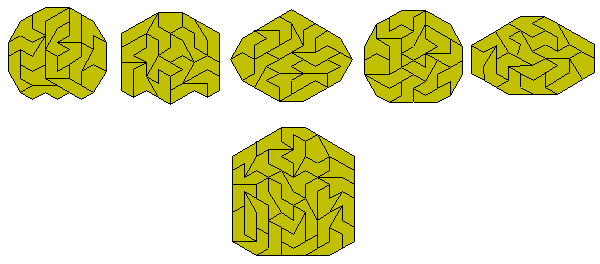
There are 17 rhombsliced tridiamonds shown here. The lower diagram is of the 32 pieces in the one-sided set.
We could also add triangles to a single rhomb (half rhombus) to give sets such as the following.
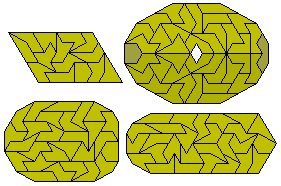
This set of 114 pieces is unbalanced and any fugure such as the one below must has a colouring excess of 4n+2.

