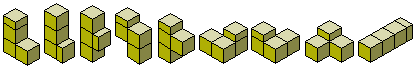Polyforms derived from the removal of half of one of the basic tiling shapes.

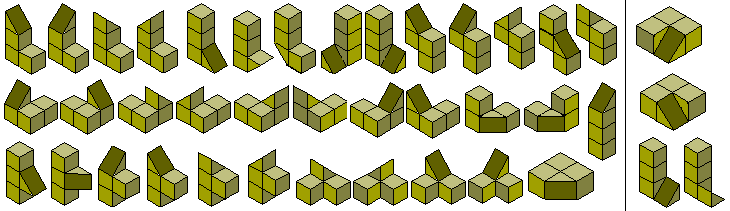
If take the set of tetrominoes and remove half a square (cut across the square) so that no original join is divided then we get the six truncated tetrominoes below.
![]()
This set is quite small and does not produce any interesting constructions. Removing a half square from the pentominoes gives us this set of 19 pieces. The only possible rectangles with the truncated pentominoes would be 4½ x 19 or 8½ x 9. Brendan Owen has shown that no solution exists for the 4½ x 19 and Patrick Hamlyn has found two solutions so far for the 8½ x 9.
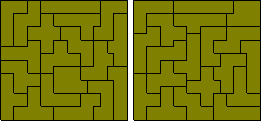
An easier problem is to make the rectangle below where one of the pieces is used twice.
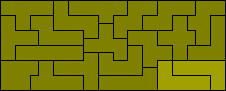
The 35 one-sided pieces shown below can also form rectangles. At least some of 2½ x 63, 3½ x 45, 4½ x 35, 5 x 31½, 7 x 22½, 7½ x 21, 9 x 17½ and 10½ x 15 are possible (the first two are not possible). The first two solutions are by Peter Esser and the three colour version of the 5 x 31½ is by Patrick Hamlyn. Peter Esser has a page on his website devoted to the one-sided truncated pentominoes.

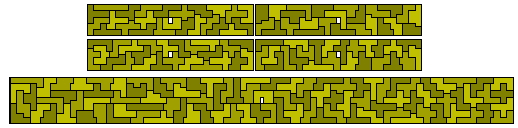
There are 67 truncated hexominoes shown here in an 11 x 33½ rectangle by Patrick Hamlyn.The only other rectangle with the correct area is a 5½ x 67 which is almost certainly not possible. The second rectangle is an 11x64 with the 128 one-sided pieces.

Another solution for the 11 x 33½ by Roel Huisman shows the symmetric pieces.

The one-sided set consists of 128 pieces which probably form a number of rectangles - 4 x 176, 5½ x 128, 8 x 88, 11 x 64, 22 x 32, 16 x 44 - with the first two at least probably not possible.
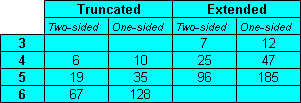
Livio Zucca has looked at sets where the half square is added to a polyomino (extended polyominoes). There are seven pieces from the trominoes (12 with the one sided set) and 25 from the tetrominoes (47 from the one-sided set).
Livio's constructions are shown below.
One-sided extended trominoes
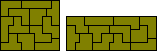
Extended tetrominoes.

Peter Esser fouind a number of pentuplications of pieces and Livio Zucca completed the solutions and produced the diagram below.

Extended pentominoes (96 pieces).