![]()
Numbers of sliced n-iamonds up to n = 8.
![]()
If we remove a half triangle from pentiamonds ensuring that no existing join is cut then we get the following 14 sliced pentiamonds which have a total area equal to each of the figures shown.
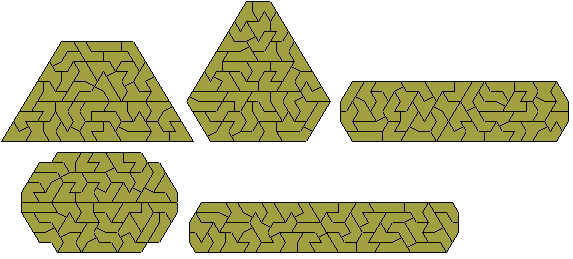
Brendan Owen has used his solver to prove that the figure at the right has no solutions and has found a unique solution to the figure at the left. Below are a number of other figures Brendan has made with this set. He found 205 solutions for the figure at the top left.
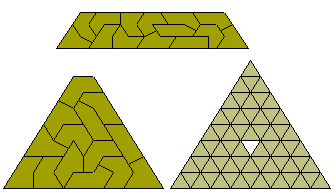
Peter Esser has now produced a polyiamond solver which can also be used with these sliced forms. Peter has found a convex figure with eight sides and asks if this is the maximum number of sides for a convex figure. The two patterns at the right have 9 and 10 sides respectively but it is not known if they can be packed with the set.
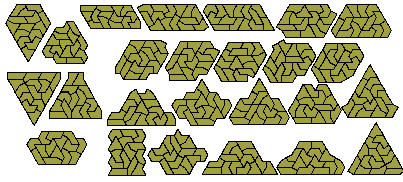
If we remove a half triangle from the hexiamonds we get the following set of 40 pieces with a total area of 220 triangles.

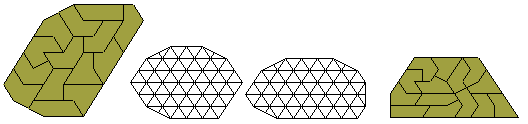
One trapezium is possible with this set as shown below together with a number of other symmetrical patterns. It is tempting to try to form a rectangle with this set however this is soon seen to be impossible once we try to fill in from a corner.