If we colour each basic tile of a polyform in all possible ways we produce chequered polyforms.
![]()
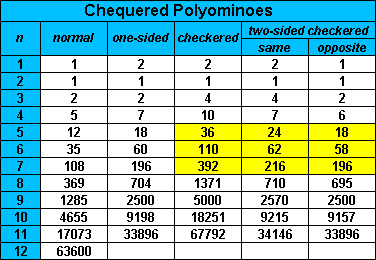
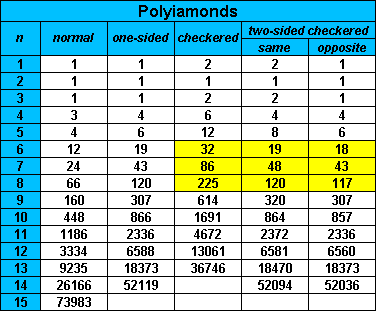
Brendan Owen has produced the following table of numbers of chequered polyominoes.
To illustrate the concept below are the three versions of the coloured tetrominoes.
| one-sided | 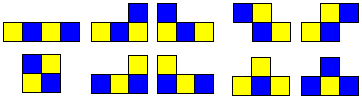 |
| two-sided (same) |
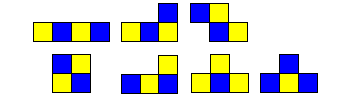 |
| two-sided (opposite) | 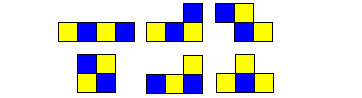 |
The figure below shows some constructions made with these sets.
The following shows some examples of the various chequered forms in a variety of solutions. In thsoe cases where the number fo squares is odd you will notice that the numbers in the above table are often double those for the unchequered set. In these cases solutions are given but many of these would also be derivable from solutions for the unchequered sets by using the solution twice with alternate colouring in each.
Isoperimetric Chequered Polydominoes
There are nine perimeter 10 same chequered pieces.
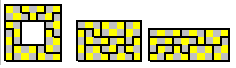
There are eight perimeter 10 opposite chequered pieces.
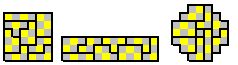
There are 47 perimeter 12 same chequered pieces.

There are 34 perimeter 12 opposite chequered pieces.
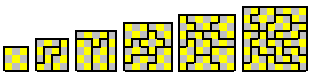
There are 39 double sided chequered tridominoes shown in three 6x13 rectangles and a 9x26 rectangle.

There are 72 single sided chequered tridominoes shown here in a variety of multiple rectangles.

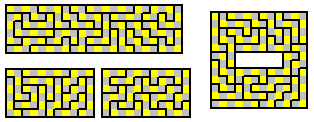
Chequered Strip Polyominoes
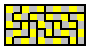
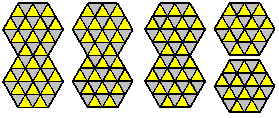
The 18 opposite chequered hexiamonds can form 6x6 or 3x18 parallelograms as well as two hexagons.

The 32 chequered-one-sided-hexiamonds are shown here in a number of constructions.
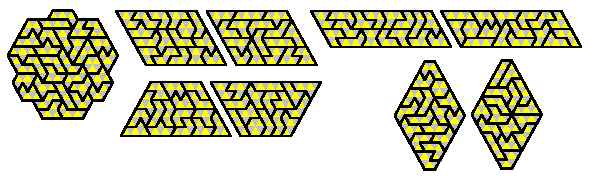
Brendan has also shown that the 32 chequered-one-sided-hexiamonds will tile all octahexes. Using the building blocks attached all 1448 octahexes can be made.
Brendan also notes that there are 30490 decahexes, 521 of these are symmetric and 69 of these can be tiled by the 12 one-sided-chequered pentiamonds. The solutions are here.
The 48 chequered-two-sided-same heptiamonds can for the two parallelgorams shown here. Again this could have been derived from the unchequered set as explained above.
The octiamonds in their two-sided opposite and same forms are shown here.
If we colour the triangles in the one-sided octiamonds in all possible ways then we get a set of 225 pieces. Ed Pegg Jr noted that this set has the right area to form a rhombus of side 30 and suggested making the rhombus with the correct colouring. Brendan Owen has finally found this solution.


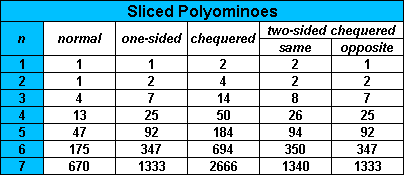
Above is a table of numbers for sliced chequered polyominoes. Below are a few examples of solutions although in these cases all of the sets have double the number of pieces of an unchequered set and so many, but not all, of these solutions are derivable from the original sets. The last few examples are from sets derived by adding squares to a sliced monomino.
Domino plus two half squares (same chequered)