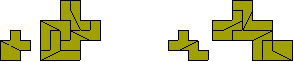Domsliced Tetrominoes

In order to make symmetric figures with the 10 domsliced tetrominoes it is
necessary to ensure that we have a design which may be possible. To check
on possibility we need to look at a chessboard colouring of the pieces. If
we look at the pieces below we see that nine have a colouring of 1¾
to 1¼ an excess of ½ whereas one piece has a 2¼ to ¾
colouring which gives an excess of 1½.
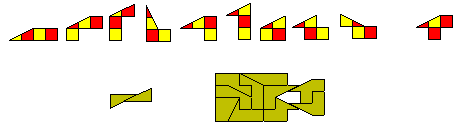
Providing that we have no cross grain joins as in the figure above,
whenever two half dominoes join they will for a domino which has a 1-1 colouring.
Thus any figure with a border purely along grid lines will have all half dominoes
joined into a domino and so the resulting figure must have a colouring excess
of 2 squares.
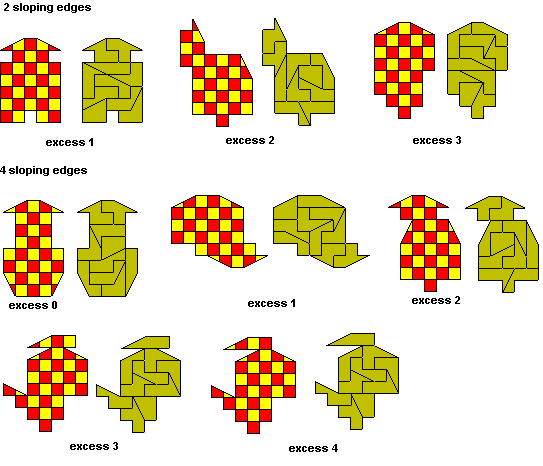
If two of the edges of the border are formed by the sloping part of the half
domino then we can have a colouring excess of 2 ± ½ ±
½ = 1, 2 or 3 and with four sloping edges we have 2 ± ½
± ½± ½ ± ½ = 0, 1, 2, 3 or 4. Examples
of each of these types are shown below.
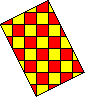
From the above we can see immediately that no rectangle following grid lines
is possible with the set. It might, however, be possible to for a sloping
rectangle such as the one below which has an area of 30 units. This also,
is seen to be impossible, however, if we consider the four edges. Firstly
no piece can contribute to more than one edge and so if we remove the edge
pieces we shall have four sloping edges and an area in the centre made up
entirely of squares. We can now join the two opposite long edges to form another
piece made up entirely of squares and finally the four pieces forming the
short edges can be joined by their colouring to form two more balanced blocks.
These four pieces will have a balanced colouring just as the figure itself
did and so we can see that no solution is possible.
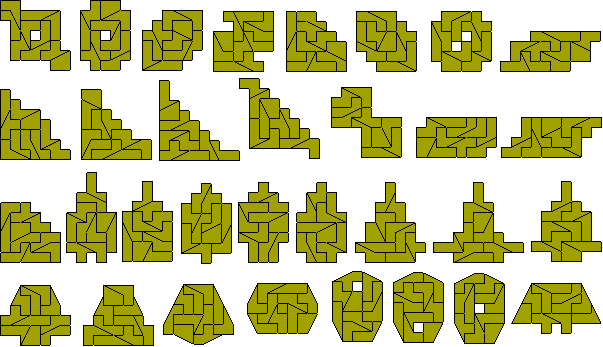
Despite all these restrictions, a number of symmetrical shapes is indeed
possible as shown here.
It is also possible to make single and duplicate copies of hexominoes. The
hexomino must be one with a 4-2 colouring and this is probably only possible
for the two shown here.
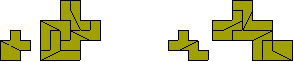
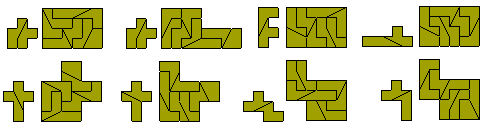
If, however, we allow the duplicated hexomino to be different from the original
then there are many more possibilities although the single sized one must
still have a 4-2 colouring.
Similar constructions can be made with two sets of pieces. This is also solvable
using the one sided set (bottom figure) but it seems likely that this may
be the only solution.
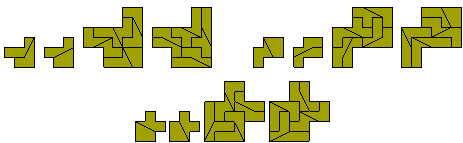
Also with the one-sided set it is possible to form quadruplicated
copies of a tetromino with a hole in the shape of the tetromino. The T-tetromino
is impossible to use because of colouring considerations.