Daniel Wyllie L. Rodrigues has suggested a new polyform based on the trikite shown below. This reminded him of an envelope flap and so the name flaptile emerged. This tile could also be seen as a half hexagon.
![]()
Other sets of pieces formed using flaptiles are shown here.
The six pieces can form a number of symmetrical shapes.
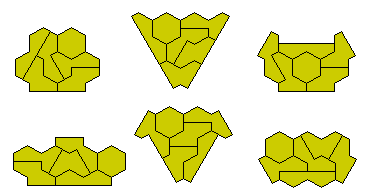
There are nine pieces in the one-sided set as shown here.
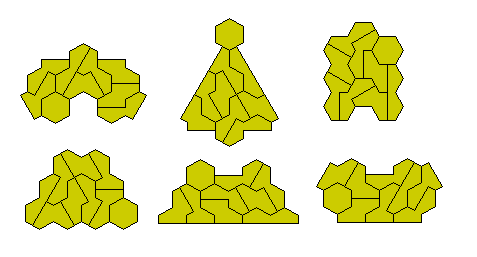
The 34 triflaptiles form a number if interesting shapes.
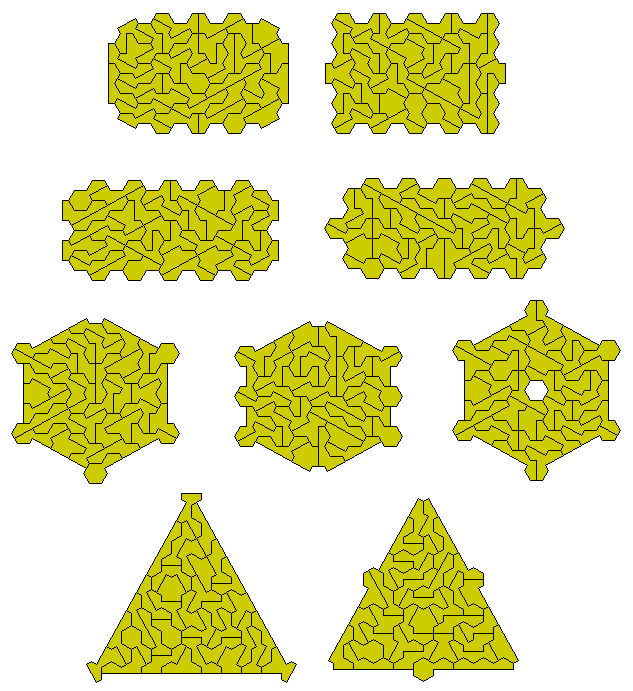
These pieces can also form congruent pairs of shapes.
The one-sided set consists of 61 pieces as shown here.
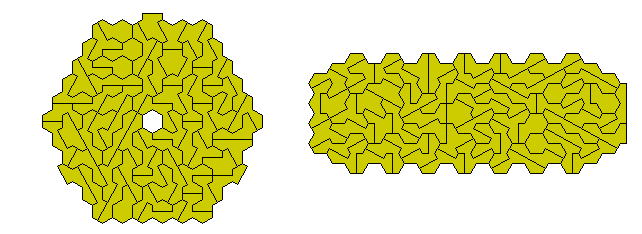
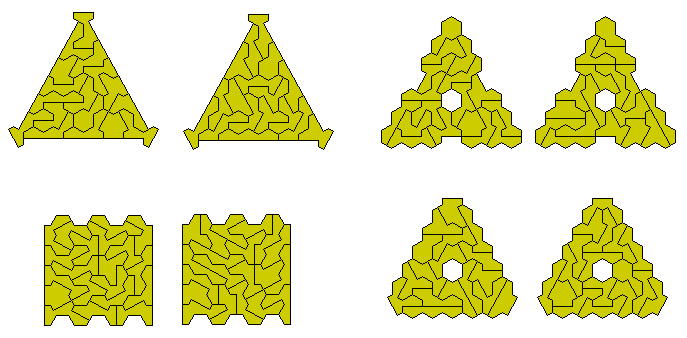
The following two constructions have a central section using the symmetric pieces with the outer parts being mirror images.
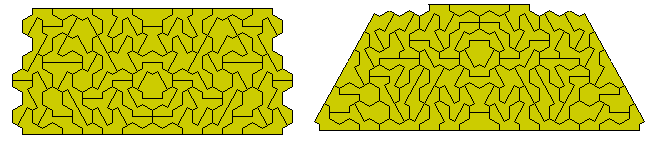
The next two colutions have a central area of symmetrical pieces and the two sides as mirror images of each other.

There are 281 pieces in the set made from four flaps.
If we use just 280 of the pieces then four congruent shapes can be made. Possibly 7 or even 14 congruent shapes could be made.
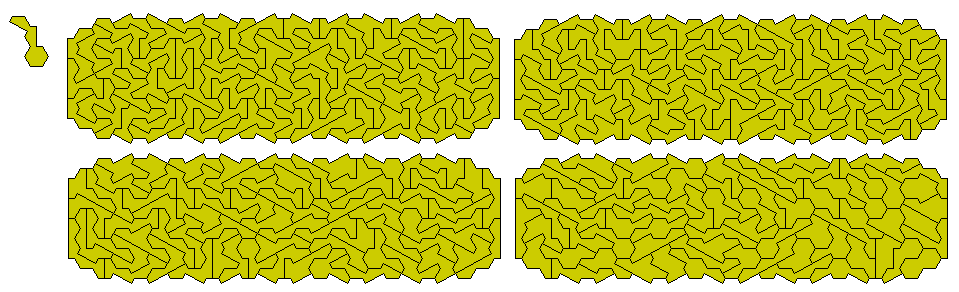
Using one piece twice three congruent figures can be made.
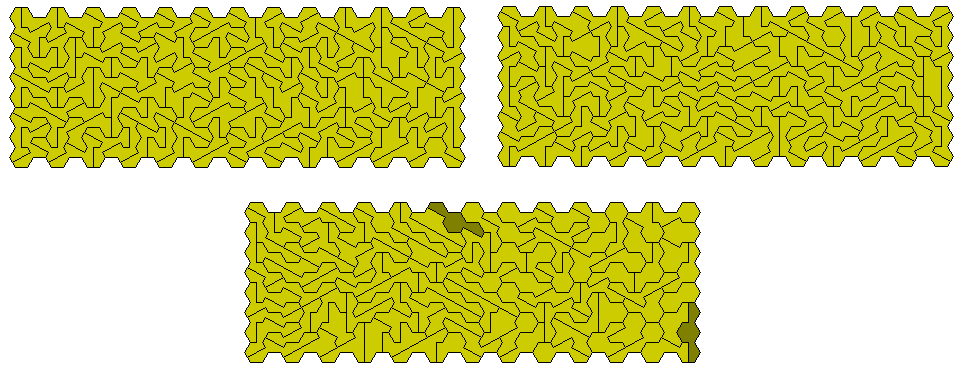
Six congruent shapes can also be made.
