![]()
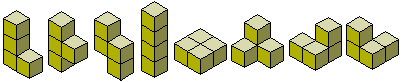
We can also look at polycubes which replicate themselves. The tetracubes (above) are all reptiles. The first four certainly form cubes of side 4 and are rep-4³ and the last four form cubes of side 2 and are rep-2³. Since the L-tetromino is rep-n² for all n it is also rep-n³. The T-tetromino is also rep-3³ as shown below.
The situation with polycube reptiles is very different from polyomino reptiles in one important aspect. For polyominoes there are no known reptiles which do not tile a rectangle but in three (and higher) dimensions Robert Hochberg and Mike Reid have shown that there exists a polycube (the 'notched' cube) which is a reptile but cannot form a box. This is shown in the diagram below. Details of their proof is in their paper 'Tiling with Notched Cubes' from Michael Reid's site.