 |
The L-tromino is a reptile as shown below where it is rep-2². It is also rep-n² for all n.

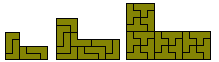
Two of the tetrominoes are reptiles. The L-tetromino is rep-n² for all k and the diagram below shows its rep-ntilings for n=2 and n=3. The T-tetromino is rep-(4n)² for all n.
Obviously all rectifiable polyominoes are also reptiles and the tromino above can be used to make a 2x3 rectangle which in turn will make a 6x6 square showing the tromino to be rep-6². However, the real problem here is to find for what values of n a figure is rep-n².
If a figure is rep-n² and rep-m² then it will also be rep-(mn)² and so we only need consider rep-p² for prime values of p and for those composite values of p where rep-k² does not exist for one or more of the factors of p. The figure below shows how the L-tetromino rep-3² can be extended to give rep-5², rep-7² and rep-9². This pattern can be extended to show the L is rep-k² for all odd k and hence for all n.