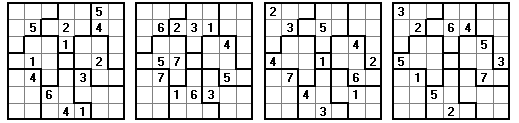
The Pentomino Sudoku Page had some examples using a 4x15 rectangle with the following conditions -
| (a) in each panel the rows contain 1 to 5; |
| (b) in each panel one number is omitted from each column. The number omitted is different in each column but the pattern of numbers omitted is the same for each panel. Thus if the numbers omitted in the first panel are, in order, 12345 then the numbers omitted in the other two panels are likewise 12345 in that order; |
| (c) no two equal numbers are next to each other |
Four more examples are given here.
This concept of omitting numbers from rows, columns or polyominoes is further explored below.
This example uses the pentominoes, omitting the 1x5 rectangle, and adds the tetrominoes to form a 5x15 rectangle. Each tetromino has one number omitted and no two equal numbers adjoin.

These problems are based on a 6x10 rectangle formed from the pentominoes with the following conditions -
| (a) In each panel columns contain the numbers 1 to 6; |
| (b) each full row contains five of the six numbers 1 to 6 with a different number omitted in each row; |
| (c) each pentomino contains five of the six numbers 1 to 6; |
| (d) no two equal numbers are next to each other. |

Here condition (b) is changed to - (b) in each panel a different number is omitted from each row and the sum of numbers in each row is 35.

Still using 6x10 rectangles but with different conditions -
| (a) In each panel columns contain the numbers 1 to 6; |
| (b) in each panel each row contains five of the six numbers 1 to 6 with a different number omitted in each row; |
| (c) each pentomino contains five of the six numbers 1 to 6; |
| (d) the numbers in each full row add to 35; |
| (e) no two equal numbers are next to each other. |

The next example uses the non-symmetric one-sided pentominoes to form a 6x10 rectangle. The red numbers show the numbers omitted from the rows in each panel. Additionally the number omitted in each pair of mirror image shapes is the same and no two equal numbers adjoin.

This next example is based on the same conditions but the red numbers indicate the omitted number in the rows and each pentomino.
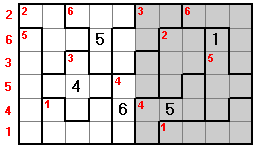
With conditions (a), (b) and (c) above these problems are based on a 6x15 rectangle made with the one-sided pentominoes.

Here the conditions are as above but the red numbers show the number omitted from each row.
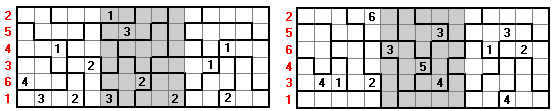
Here we have a 5x18 rectangle made with the one-sided pentominoes with conditions -
| (a) in each panel the rows contain 1 to 6; |
| (b) in each panel one number is omitted from each column. The number omitted is different in each column but the pattern of numbers omitted is the same for each panel. Thus if the numbers omitted in the first panel are, in order, 12345 then the numbers omitted in the other two panels are likewise 12345 in that order; |
| (c) no two equal numbers are next to each other |
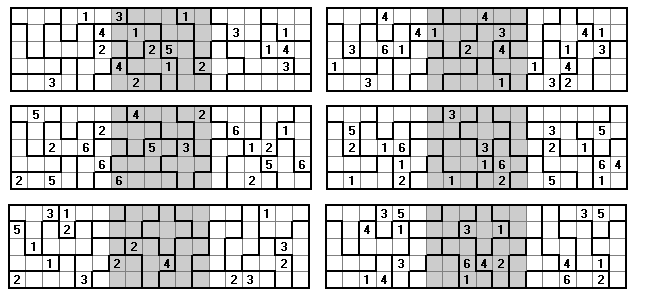
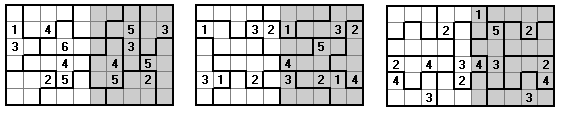
Here we have 6x10 rectangles formed from two different pentoimoes.
| (a) in each panel the columns contain 1 to 6; |
| (b) one number is omitted from each row in each panel; |
| (c) no two equal numbers are next to each other; |
| (d) each set of six congruent pentominoes has a different number omitted from each piece. |

Here we have the same as above but now one number is omitted from each full row.
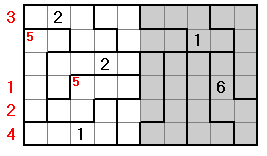
As above but here the numbers in red indicate numbers which are missing from rows or pentominoes.
Here again (a) to (d) above but with the additional condition that each row adds to 35.

Next we have 6x15 rectangles formed from three different pentoimoes.
| (a) in each panel the columns contain 1 to 6; |
| (b) one number is omitted from each full row; |
| (c) no two equal numbers are next to each other; |
| (d) each set of six congruent pentominoes has a different number omitted from each piece. |
| (e) no two equal numbers are next to each other. |

Next we have 7x12 rectangles with conditions -
| (a) In each panel columns contain the numbers 1 to 7; |
| (b) in each panel each row contains six of the seven numbers 1 to 7 with a different number omitted in each row; |
| (c) each hexomino contains six of the seven numbers 1 to 7; |
| (d) no two equal numbers are next to each other. |

This next example uses a 7x12 rectangle made copies of two hexominoes with conditions
| (a) In each panel columns contain the numbers 1 to 7; |
| (b) in each panel each row contains six of the seven numbers 1 to 7 with a different number omitted in each row; |
| (c) each hexomino contains six of the seven numbers 1 to 7; |
| (d) the T shaped pieces each contain only two even numbers; |
| (e) no two equal numbers are next to each other. |

Here we have a 7x7 grid made up of seven hexominoes and a single central square. Each row and column contains the numbers 1 to 7 while each hexomino has six of the seven numbers.