Hexomino Constructions
Below are a number of constructions made with full set of 35 hexominoes. The 'rhombus' shape at the bottom is by David Bird and the one at the top right is by W. Stead.
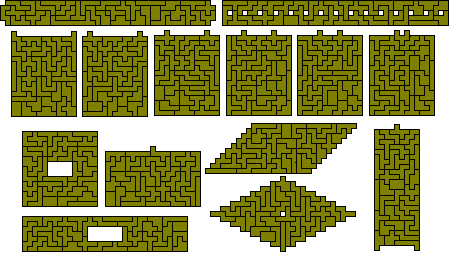
The 5-7 and 7-5 problems
With a total of 35 pieces it might be possible to make 5 congruent shapes consisting of seven pieces or 7 congruent shapes with 5 pieces each. Both of these are possible as can be seen from the following courtesy of Mike Reid.
The Sextuplication Problem
Below are some solutions to this problem. This requires a sixfold replica of the hexomino to be built with the sextuplicated piece used twice in the solution. This can only be done for those hexominoes with a 4-2 chessboard colouring.

The 1-3-5 and the 1-3-3-4 Problems
These problems are based on the fact that 12+32+52 = 12+32+32+42 = 35 and give simultaneous constructions of various sized copies of one of the colour unbalanced pieces. It might just be possible to form similar sets based on 12+22+22+22+22+32+32=35 but this seems unlikely.


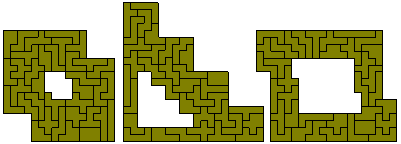
The similar hole problem
Here the problem is to create an hexomino construction with a hole of a similar shape. One solution is the sextuplication problem above. The other solutions below show the other three possible hole sizes - 14, 40 and 70 - as well as solutions to a two similar holes problem. These were made by Jean Meeus.
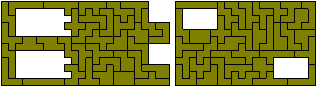
Mike Reid has recently found another solution

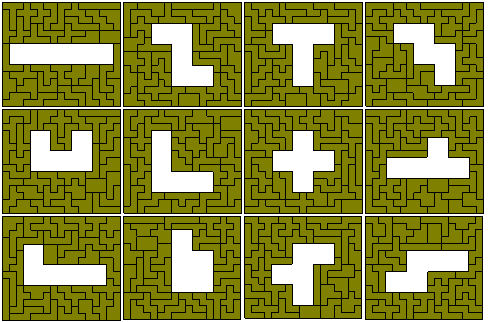
Jean Meeus also proposed forming a 15x17 rectangle with a hole in the shape of a triplicated pentomino. All 12 problems are possible as shown below - the first six solutions are his and the solution for the X-pentomino is by Pieter Torbijn.
Here the problem is to find a figure with the maximum number of unit holes. The greatest known number is 50 although up to 56 may just be possible. The figure at the left was made by hand in the 1970s but Patrick Hamlyn has improved on this with two solutions where the 50 holes are in a rectangle. This is the maximum number which can be put into a rectangle.
Dominique Mallet has increased the number of possible holes to 52. Below are her solutions - five 50 hole; six 51 hole; and two 52 hole patterns.
The 15x15 problem
Another problem would be to form a 15x15 square with the addition of three pentominoes. One solution is shown below. The one with three F-pentominoes was found in under three minutes using Gerard's Universal Polyomino Solver but the one with the T-pentominoes took longer - about 15 minutes.
All the other pentominoes can also be used as shown here.

Alternatively you may decide to do these problems by hand and produce solutions such as those below where the pentominoes are placed in some pattern. These solutions took under 30 minutes each by hand.

One-sided Hexominoes
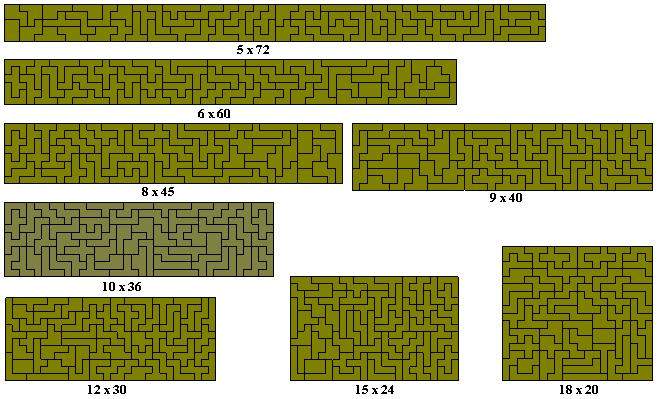
If we consider mirror image pairs as distinct then there are 60 hexominoes. With this set we have an even number of unbalanced (4-2 colouring) pieces and so rectangles may well be able to be formed. The possible rectangles would be 3x120, 4x90, 5x72, 6x60, 8x45, 9x40, 10x36, 12x30, 15x24, 18x20. The 3x120 is not possible as can be seen from the diagram below where one of the hexominoes must divide the rectangle into two parts neither of which contains a multiple of six squares.
The 4x90 is also impossible as can be seen by considering the contribution each piece can make to the long edges. These require a total of 180 but the maximum possible with a full set is 165 (in calculating this we must be aware that any piece which crosses the rectangle must divide it into areas which are multiples of 6.
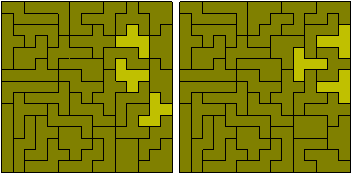
All of the other rectangles are possible as shown here.
Mike Reid has found alternative solutions to these by means of forming multiple rectangles with the full set.
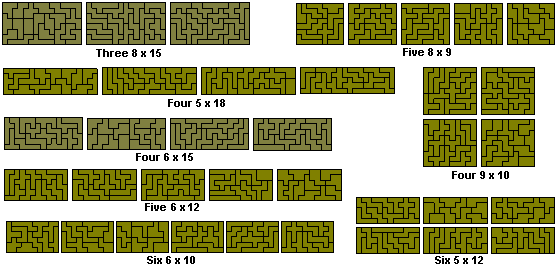
The above were all done by hand. By contrast here are some of the same rectangles from Patrick Hamlyn solved by computer.

A number of other patterns are possible with this set such as the two 'squares' shown here. The second one of these could also be formed from the four 9x10 rectangles above. The figure at the top right is by David Bird.

The last construction above (three 6x12 rectangles and four 6x6 squares) would allow the sextuplication of any of the dekominoes.
Brendan Owen has packed the set into ten congruent shapes and Patrick Hamlyn has found 12.
One problem for this set is that of octuplication with a similar duplicated hole. This should be possible for all pieces.

You will probably have noticed that the hole in the rectangle above is not exactly central. Mike Reid has fixed this and produced some other solutions.
There are many more possible similar hole problems for this set and these are discussed on a separate page.
As with the 1-3-5 and the 1-3-3-4 problems above, a variety of multiple sized copies of pieces can be made with the set. Other possibilities for which no solution is known include 2-2-2-2-2-2-2-4-4 and 2-2-2-2-2-2-3-3-3-3.