If we remove the pieces with holes we get a set of 363 pieces.

Unfortunately this set is unbalanced (chessboard colouring) and so no rectangles is possible. Eleven congruent shapes can, however, be made.

Patrick Hamlyn has improved on this by finding 33 congruent shapes.

Also possible with this set is to make three 11-fold replications of an unbalanced octomino.

Patrick Hamlyn has produced the following construction which, by rotating the various sections, will produce solutions to the above problem for a number of the unbalanced octominoes. Some examples of the other pieces formed are shown below.

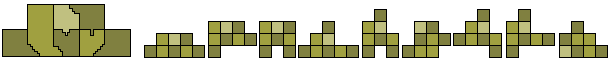
There are 227 octominoes which are chessboard balanced (4-4 colouring) and it is tempting to try to form a rectangle with these pieces. Unfortunately this is not possible since if we colour the possible rectangles by strips we find that and odd number of the pieces cover an unbalanced colouring.
for octominoes , and other n-ominoes with n divisible by 4, we have these parities:
12-21
this notation means that we tile the plane with aligned
squares with colors 1 and two, the first row is (1,2), the 2nd row
is (2,1) |
||
Parities
are determined by a total of an even number of pieces of each colour. |
||
1 |
12-21 |
230 non-holey 8ominoes have parity1=0 and 133 have parity1=1 |
2 |
11-22 |
this is rotation invariant, iff parity1=0 |
3 |
12-34 |
this is invariant, iff parity1=0=parity2 |
4 |
1122-1122-2211-2211 |
this is invariant, iff parity1=0=parity2 64 of the 124 pieces above have parity4=0 , (not the same pieces as in (3), 25 have parity3!=parity4 ) |
5 |
1122-1122-1122-1122 |
|
6 |
1122-1122-3344-3344 |
|
7 |
1234-2341-3412-4123 |
121 pieces where this is well-defined, 72 pieces where all counts are even, 49 pieces. where all 4 counts are odd |
8 |
1234-3412-1234-3412 |
|
9 |
123-231-312 |
78 pieces where all 3 counts are even no odd pieces here, the other 152 pieces have non defined parity(9) |
10 |
123-123-123 |
|
The colourings corresponding to the above are shown here.

It would seem tempting to try to make a rectangle with the 227 balanced pieces. Unfortunately this is not possible as proved below.
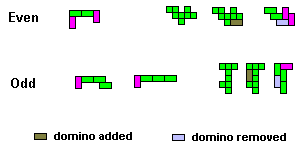
Classify the balanced pieces as even if they can be divided up into dominoes with an even number in each direction and odd if they are 1-3 in direction. For those which cannot be divided into dominoes add a domino so that the new shape can be divided into dominoes . In this division remove one domino that is in the same orientation as the added domino and then classify as before (see examples below). This gives an odd number of odd pieces and since any rectangle will be even no rectangle can be made
Any symmetrical figure made with the set will have either (a) an axis of symmetry parallel to the grid lines; (b) a diagonal axis of symmetry; or (c) rotaional symmetry. Noting that any construction must be tilable by an odd number of dominoes in each direction and considering the three cases we see
(a) If the axis of symmetry is along a grid line then the figure can be tiled by dominoes all in the same direction. If, however, the axis is along the centre of squares then removing this central line of squares and joining the two sections will produce an area which can be tiled by dominoes in the same orientation. Now the removed section being a single line of squares must consist of an even number of dominoes and so in neither case can the figure be filled.
(b) Diagonally symmetric figures with odd numbers of dominoes in both directinos can be made as in the example below.
(c) If the figure has rotational symmetry then if we divide the figure along a line through the centre of rotation and reflect one half we get a type (a) figure. Since no domino has been rotated in this operation there will again be an even number in both directions.
Patrick Hamlyn has produced the following construction using the 136 unbalanced pieces.

