Suppose you have a deck of n cards, labelled with numbers from 1 to n. You start counting the cards 1,2,3... If the count does not correspond to the number on the card on top of the deck, you move the card at the end of the deck. Otherwise, you put the top card aside and start counting again from 1.
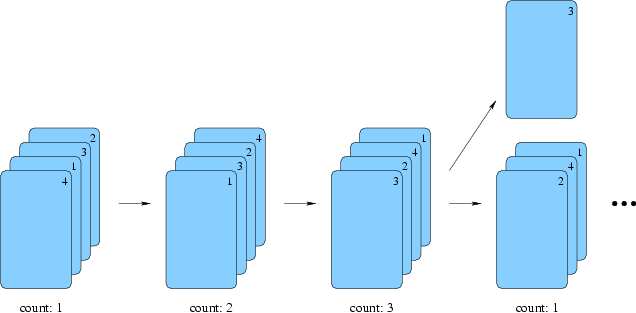
If your count reaches n+1, then you have lost, your deck is a dead-end and the game stops (this would happen by continuing the above example game). Otherwise, if you were able to remove all the cards with this method, then it is a success, and you restart the whole procedure on a new deck of cards, in the order in which you removed the cards.
For example, for n=4, if you start from the deck 1 4 3 2, you start by removing the 1, then you count 1,2,3,4, you remove the 4, then 1,2, and finally 1,2,3 on the last card. This gives you the new deck 1 4 2 3.
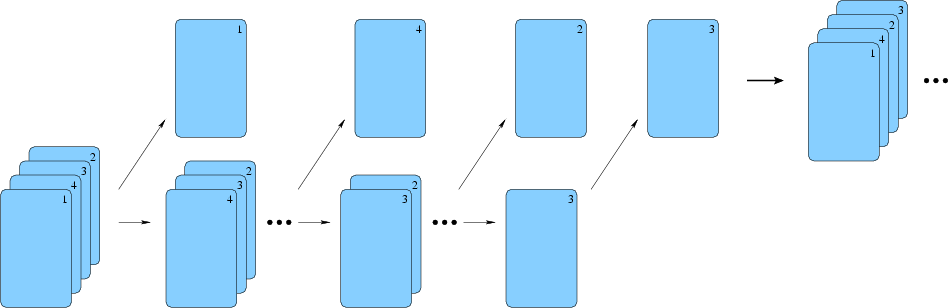
Starting again, you remove in order 1 2 3 4. Starting again, you remove the 1, but cannot remove any other card, so the game stops here.
Two cases can occur: either you reach a dead-end at some point, or you fall into a cycle, meaning that you get a previously encountered deck.
THE MODULAR MOUSETRAP
In this variant, you count modulo n. This means that you do not stop at n+1, but continue counting again with 1. Some decks are still dead-ends, like for example 4 3 2 1 (you would be counting infinitely without ever removing any card). Again, you continue playing until you reach either a dead-end or a cycle.
For example, starting from 1 3 4 2, you would remove the 1, then count 1,2,3,4,1,2, remove the 2, and finally remove the 3 and 4. You would get the new deck 1 2 3 4. On this one, you would remove the 1, then count 1,2,3,4,1,2,3,4,1,2, and remove the 2, and finally remove the 3 and 4. You would get again 1 2 3 4, and thus stop because you ran into a cycle (this cycle is trivial, but there may be non-trivial cycles).
WHAT YOU HAVE TO DO
You have to provide 30 initial decks that produce long sequences and that preferably run into a cycle. More precisely, you have to provide decks for both the non-modular and modular versions for values of n from 10 to 25, except for 23 (guess why, designers of programming contests have strange requirements sometimes...).
THE SCORING
The length of a sequence is the number of distinct decks (including the starting one) you encounter before reaching either a dead-end or a previously encountered deck. This means that for cycles, this might be the length of the initial steps, plus the length of the cycle itself. For example, the length of the sequence starting from 1 4 3 2 in the non-modular version is 3, and the length of the sequence starting from 1 3 4 2 in the modular version is 2. More generally, the sequence A B C D E E E E... has length 5 (4+1), and the sequence A B C D E C D E C D E... has length 5 (2+3) (where different letters denote different decks).
For each category, only your "best" entry is considered for the scoring. "Best" means your longest entry with cycle if you have entries with cycles, otherwise your longest entry if all your entries are without cycles. For each category, the reference length is the longest length among the best entries of all participants (the cyclic aspect is not taken into account here). Then, for each category, you get an individual subscore which is the length of your best entry divided by the reference length. Moreover, since cycles are good, you get 1 extra bonus point if your best entry ends on a cycle. As a consequence, a subscore is a number between 0 and 2. Note also that a cyclic sequence is always considered better than a non-cyclic one, even if it is much shorter. So if your best entry is a cycle of length 3, while another participant has a non-cyclic sequence of length 10 as his best entry, you get 1+3/10 = 1.30 points for that category, while he gets only 0+10/10 = 1 point.
Your global score is the sum of the 30 subscores. It is a number between 0 and 60.
HOW TO SUBMIT ENTRIES
First of all, you have to register in order to get your account created.
Then, you can go to the submission page (username and password required), and fill the form with you entry. For convenience of use, your entry will be processed both in the non-modular and in the modular categories (but there is little chance that a same entry gives a good scoring in both categories). After submission, the lengths of the sequences starting from your permutation are computed and eventual cycles are detected.
Important: In the modular category, for values of n of 17 and 19, the entries will not be processed immediately by the web server, but will be processed manually from time to time (I hope every couple of days). This is necessary because those entries might take too much time and I don't want to overload the server. In your My entries page, will you be able to see if your entries have been processed. So, please don't write me e-mails to tell me that your score wasn't updated after you submitted a modular entry for n=17 or 19, and just be patient. On the general Standings page, will you also see the date of the last manual processing.
Very important: In order to avoid overloading the server, you must not use the submission page to compute the length of your sequences. You should only submit what you assume to be your best solutions. I will disqualify any person who submits an "unreasonable" number of entries.
OTHER RULES
Here are a few other rules:
- You cannot have multiple accounts or enter the contest more than once.
- Teams are allowed. However, once you are in a team, you cannot re-enter the contest as an individual, and conversely once you are registered as an individual, you are not allowed to join a new team. Moreover, the composition of teams cannot be changed after their creation. Please indicate the names of all participants when registering.
- People from Aarhus University are not allowed to join the contest.
- How ties are resolved: when two entrants get exactly the same score, the tie is resolved by looking at the time of their last entry (the older one gets first). If there is still a tie, the first will be the one with the lower number of entries.
- I am in no way responsible of collateral damages induced by this contest. This includes, but is not limited to: soulmate quitting the house because you spent your nights on the contest, boss getting angry because you are using all the CPUs of all your co-workers, etc...
DISCUSSION GROUP
If you want to discuss about this contest, please join the Mousetrap Programming Contest mailing list. Any kind of discussion is allowed, provided it has a direct link with this contest. You are free to post your results, entries or code (but of course you might not want to reveal your secrets until the end of the contest).
If you have questions about this contest or a technical problem, please post a message to this list instead of sending an e-mail directly to me, as some other participants might help you faster than I can.
Official announcements about this contest will also be made on this list (and also on Al Zimmermann's discussion group).
REFERENCE
The game of mousetrap was invented by Cayley (there is a reference to it in MathWorld). For those of you who have access to it, this problem is inspired by the section E37 of Richard Guy's book "Unsolved problems in number theory".
Back to the main page.