Al Zimmermann's
Squares Programming Contest
First Prize: $500 Second Prize: $50 The contest has ended.
The results are available here.
THE SQUARES PROBLEM
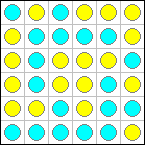
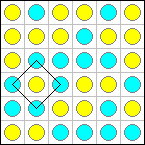
You have a square grid of size n by n. You also have unlimited supplies of stones in each of two colors. Place a stone on each cell of the grid. For example:

Now try to find 4 stones of the same color which form the corners of a square. We call such squares ďmonochromaticĒ. In the above example there are exactly three monochromatic squares:
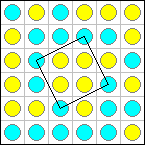
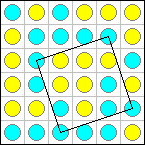
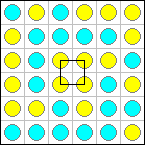
The Squares Problem for a given n is to find an arrangement of stones that forms as few monochromatic squares as possible.
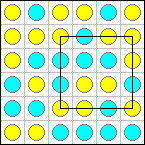
For example, the following arrangement of stones is a better solution for n = 6 than the above example because it has only 2 monochromatic squares.
THE CONTEST
Email me (see How To Enter, below) your best grids for values of n from 7 to 31. Iíll calculate a subscore for each grid (details of the scoring system are below) and the total of your 25 subscores will be your contest score. The person with the highest contest score wins. In case of a tie, the prize goes to the person who achieved the winning score first.
THE PRIZES
First prize is $500. Second prize is $50.
HOW TO ENTER
Send an email containing your entry to bitzenbeitz@aol.com before Noon GMT on December 6, 2003. Put just the word SQUARES in the subject line. The body of the email should be formatted exactly as follows.
Additional spaces and line breaks may be included anywhere (except in your name and location) to improve readability.
Do not include any extraneous information anywhere in the email. Do not send any grids smaller than n = 7 or larger than n = 31.
Scoring will be done by computer, so be careful in composing your email.
Thereís an example of an entry in the Frequently Asked Questions section, below.
You may enter as often as you like (see The Scoring System below), but you are only eligible to win one prize.
THE SCORING SYSTEM
Each time you submit an entry I will merge it with your prior entries, if any. The result will be a virtual entry containing your best grid for each of the 25 sizes. I will give each of these 25 grids a subscore from 0 to 1 and their sum will be your contest score.
I score the individual grids as follows. If your grid is the best grid that was submitted for that grid size, I give it 1 point; otherwise I give it only a fraction of a point. The fraction is the smallest number of monochromatic squares for that grid size, divided by your number of monochromatic squares. For example, suppose your grid of size n = 7 has 5 monochromatic squares. Further suppose that the best grid that was submitted to the contest (for the same size) has 2 monochromatic squares. Then your subscore for that grid is 2 / 5 = 0.4.
GETTING YOUR QUESTIONS ANSWERED
First, check the FAQ section below. If you can't find the information you need there, send your question to the discussion group. If your question is of a personal nature, you can send email directly to alzimmerma@aol.com.
THE DISCUSSION GROUP
If you think you might enter the contest, it is important that you join the contest discussion group. You can join either by sending a blank email to this address or by clicking here. The discussion group serves two purposes. First, it allows people to ask for clarifications to the rules. Be aware that sometimes these requests result in changes to the rules, and the only place those changes are announced is in the discussion group. Second, the discussion group allows contestants to interact with each other regarding programming techniques, results and anything else relevant to the contest.
ACKNOWLEDGMENT
This contest was inspired by a game invented by John Conway and described in a Martin Gardner Mathematical Games column.
MY LAWYER WOULD WANT ME TO SAY THIS
I reserve the right to discontinue the contest at any time. I reserve the right to disqualify any entry or entrant for any reason that suits me. I reserve the right to interpret the rules as I see fit. I reserve the right to change the contest rules in mid-contest. In all matters contest-related, my word is final.
FREQUENTLY ASKED QUESTIONS
Can you give an example of a valid contest entry?
To save space, letís assume that the entry contains grids only of sizes n = 4, 5 and 6. Here's how an entry might look:
0110
1001
1100
1010.
11010
00011
01100
00110
11010.
110010
011000
000111
011000
100110
110010.
#
Robert Squarepants
Four Corners, Oregon, United StatesYou could also format this entry more compactly as follows:
0110100111001010.
1101000011011000011011010.
110010011000000111011000100110110010.
#
Robert Squarepants
Four Corners, Oregon, United StatesDo I have to submit a grid for every n from 7 to 31?
No. And yes.
Individual entries do not have to contain all 25 grids. If you send an email with fewer than the 25 grids, your grids will still be validated and recorded in the contest database. However, until I have received at least one grid of each size from you, you will not receive a score and you will not be listed on the contest standings page.
How will I know that youíve received my entry?
When I receive an entry I process it with the automated Parser/Scorer and then send a confirmation back to the submitter. Although the Parser/Scorer is automated, the process of getting entries into the Parser/Scorer is not, so it may take as long as 24 hours for you to receive your confirmation.
Iím going to join the contest discussion group. Are there any topics that are prohibited there?
Naturally, postings should pertain to the contest. But there are a couple of additional restrictions. First, you canít post solutions (that is, grids with arrangements of stones on them). If you want to tell everyone how few monochromatic squares youíve got in your size 31 grid, go right ahead Ė just donít show them the grid itself. Second, you canít post computer programs. These restrictions are lifted after the contest ends.
How can I find out the subscores for my individual grids?
You canít find out the subscores for your individual grids. Furthermore, if you try to manipulate the entry submission and scoring process in an effort to deduce them youíll be summarily dropped from the contest.
Squares Contest Final Results ó Al Zimmermann's Programming Contests
You are visitor
to this site.