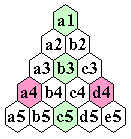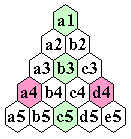| 15 Hole Triangular Board |
|
|
|
|
| Single Vacancy
to Single Survivor Problems |
|
| # |
Vacate |
Finish
at |
Length of Shortest Solution |
Number of Solutions |
Longest Sweep |
Longest Finishing Sweep |
Shortest Longest Sweep |
Number of Final Moves |
#(Longest, Second longest,
Final) [Comment] |
| 1 |
(0,0) |
a1 |
(0,0) |
a1 |
10 (S) |
15 |
3 |
3 |
3 |
4 |
15(3,2,3) |
| x |
(1,-2) |
b3 |
(0,0) |
a1 |
Impossible |
0 |
|
|
|
|
|
| 2 |
(0,-3) |
a4 |
(0,0) |
a1 |
10 |
15 |
3 |
3 |
3 |
4 |
15(3,2,3) [Same as #1] |
| 3 |
(2,-4) |
c5 |
(0,0) |
a1 |
9 (S) |
6 |
3 |
3 |
3 |
4 |
2(3,3,3), 4(3,2,3) |
| x |
(0,0) |
a1 |
(1,-2) |
b3 |
Impossible |
0 |
|
|
|
|
|
| x |
(1,-2) |
b3 |
(1,-2) |
b3 |
Impossible |
0 |
|
|
|
|
|
| x |
(0,-3) |
a4 |
(1,-2) |
b3 |
Impossible |
0 |
|
|
|
|
|
| 4 |
(2,-4) |
c5 |
(1,-2) |
b3 |
10 (S) |
5 |
2 |
2 |
2 |
1 |
5(2,2,2) |
| 5 |
(0,0) |
a1 |
(2,-4) |
c5 |
10 (S) |
16 |
4 |
4 |
2 |
4 |
1(4,1,4), 1(3,2,1), 10(2,2,2), 4(2,2,1) |
| 6 |
(1,-2) |
b3 |
(2,-4) |
c5 |
11 (S) |
5 |
2 |
1 |
2 |
1 |
5(2,2,1) |
| 7 |
(0,-3) |
a4 |
(2,-4) |
c5 |
10 |
16 |
4 |
4 |
2 |
7 |
1(4,1,4), 1(3,2,1), 10(2,2,2), 4(2,2,1) [Same as #5] |
| 8 |
(2,-4) |
c5 |
(2,-4) |
c5 |
9 (S) |
15 |
5 |
5 |
2 |
8 |
3(5,1,5), 3(4,2,4), 1(3,3,3), 1(3,2,3), 2(3,2,2),
5(2,2,2) |
| 9 |
(0,0) |
a1 |
(0,-3) |
a4 |
11 |
16 |
2 |
1 |
2 |
1 |
16(2,2,1) |
| x |
(1,-2) |
b3 |
(0,-3) |
a4 |
Impossible |
0 |
|
|
|
|
|
| 10 |
(0,-3) |
a4 |
(0,-3) |
a4 |
11 |
8 |
2 |
1 |
2 |
1 |
8(2,2,1) |
| 11 |
(3,-3) |
d4 |
(0,-3) |
a4 |
11 |
8 |
2 |
1 |
2 |
1 |
8(2,2,1) |
| 12 |
(2,-4) |
c5 |
(0,-3) |
a4 |
10 |
8 |
3 |
2 |
2 |
2 |
2(3,2,1), 1(2,2,2), 5(2,2,1) |
| |
|
|
|
|
Total: |
133 |
|
|
|
|
|
| Column
Definitions: |
|
|
|
|
|
|
|
| Length of
Shortest Solution |
This is the length of the shortest solution to
this problem, minimizing total moves |
| Number of
Solutions |
|
This is the number of unique solution
sequences, irregardless of move order and symmetry |
| Longest Sweep |
|
|
This is the longest sweep possible in any
minimal length solution [link to solution] |
| Longest
Finishing Sweep |
This is the longest sweep in the final move of
any minimal length solution [link] |
| Shortest
Longest Sweep |
There is no minimal length solution where all
sweeps are shorter than this number [link] |
| Number of Final
Moves |
This is the number of different finishing moves
(up to symmetry) |
| #(Longest, Second Longest, |
Eg. 12(8,7,2) indicates there are 12 solutions
with different move sequences, where |
|
|
|
|
|
, Final) |
the longest sweep is 8, the second longest
sweep is 7, and the final sweep is 2 |
| (S) Problem is
symmetric, multiple solutions counted as one |
|
|
|
| Solution
differences can be very subtle. |
|
|
|
|
|
| Download a text file with all 133
solutions |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Triangular Peg Solitaire Main Page
