Magic Star Puzzles

The following pictures were sent to me by Jerry Slocum of Beverly Hills, CA, USA in September, 2002.
They are taken from magic object puzzles in his large collection of mechanical puzzles.

It is unfortunate that, while some of these puzzles are very old, they do not usually show a date.
Did you notice the prices?.
The 'Marvellous' "26" puzzle, in particular, seems to be of circa 1900 origin. However, while much is made of the fact it is copyrighted, no date is show.

These puzzle pictures were supplied courtesy of:
Jerry Slocum and the non-profit Slocum Puzzle Foundation. Thank you, Jerry, for supplying me with this material.
And thank you, Paul Vaderlind, for putting me in touch with Jerry Slocum.



		See my previously published material on the magic Hexagon here. Especially as regards to credits.

The following six pencil-and-paper puzzles were also received in the package sent by Jerry Slocum. They are selected from 22 such puzzles which are credited to Ivan Moscovich,1995. However, none of them appear in any of the four books I have at hand by this author.

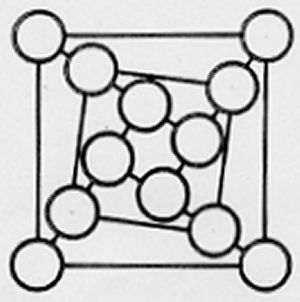Magic Triple Nesting Square
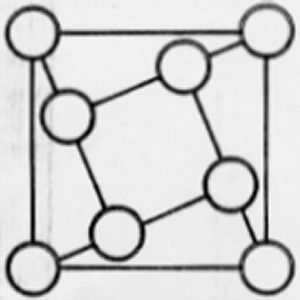
Distribute numbers from 1 to 12 to get the same sum in 4 linear tetrads and 4 squares.

Magic Whirling Squares
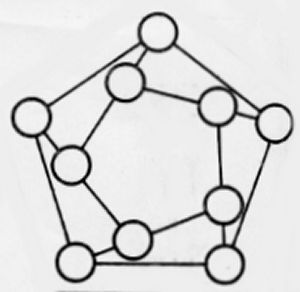
Distribute numbers from 1 to 8 to get the same sum in 4 linear tetrads and one square sum double the other.

Magic Whirling Pentagons
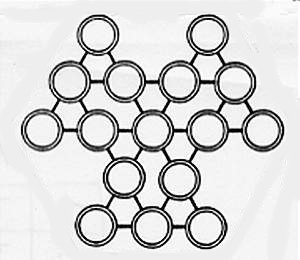
Distribute numbers from 1 to 10 to get the same sum in 5 linear triads.

Magic Triangles Pinwheel
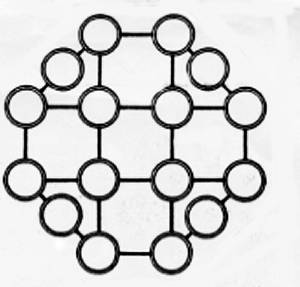
Distribute numbers from 1 to 16 to get the same sum in 3 linear triads, 3 linear tetrads, and 3 linear pentrads.

Magic Octagon Cross
Distribute the numbers 1 to 16 to get the same sum in 4 linear triads and 4 squares.

Magic Nesting Triangles
Distribute the numbers 1 to 12 to get the same sum in 6 tetrads.

I have not yet achieved solutions to all of the 6 puzzles shown above, so cannot guarantee that such solutions do exist. I would be interested in hearing of results obtained in this regard.

Is there an interest out there for a page (or pages) of number puzzles such as the six shown above?

The above images were all contributed by Jerry Slocum and I thank him again for his kind generosity.
If I receive additional material of this type from other sources, I will add it to this page.

Please send me Feedback about my Web site!