 |
 |
 |
 |
 |
 I hope you find find this page interesting and informative. I will be adding
to it from my notes and future studies as time permits so please come back often.
I hope you find find this page interesting and informative. I will be adding
to it from my notes and future studies as time permits so please come back often.
So far, I have been concentrating mainly on finding the basic solutions for the different orders. There is much left to discover about the characteristics of the individual orders. Share with me the excitement of the search.
If you are also interested in Magic Stars, I would like to hear from you.
March 1, 2005 NEW 4 pages added. See
bottom of contents!
April 4, 2007 NEW (page 9x5 stars) added. See
bottom of contents!
May 18,2007 New section on early solvers added to
Order 6 Stars.
![]()
Introduction |
A basic definition of Magic Stars and the
similarity to Magic Squares. Includes a diagram of the 3 Order-9 patterns and shows the
order that numbers are assigned to the lines. |
Basic and Equivalent Solutions |
An explanation of which solutions are considered basic
and which are equivalent solutions. The two requirements for a basic solution and converting an equivalent to a basic solution. |
Complements and Index Numbers |
Each solution has a complement. If the
solution is basic the complement is an equivalent and must be normalized to arrive at it's
basic solution. Includes a diagram of four Order-6 solutions to illustrate the above. |
Examples of Magic Stars |
Sixteen different diagrams from Order-5 to Order-11d Also shown is the solution number and the total number of solutions. |
Examples of Magic Stars - 2 |
Sixteen different diagrams from Order-12a to Order-14e. Also shown is the solution number and the estimated total number of solutions. |
Big Magic Stars |
1 solution for pattern A of orders 15 to 20. Also blank graphs of the other patterns for each order. |
A magic Star Definition. |
What is a Magic Star? Here is a formal definition and
an explanation of terms used in my discussion of magic stars. Included also are comparisons between the different orders. |
Order-5 Magic Stars |
Order-5 is not a pure magic star but there are 12 solutions
using numbers 1 to 12 but omitting numbers 7 and 11. Another 12 solutions leave out the 2
and 6. |
Order-6 Magic Stars |
A list of the 80 basic solutions along with characteristics.
20 sets of 4. Super-magic stars. A tribute to H. E. Dudeney. |
Order-7 Magic Stars |
General characteristics. Lists of the 72 basic
solutions for each of the 2 patterns. |
Order-8 Magic Stars |
General characteristics. Lists of the 112 basic
solutions for each of the 2 patterns. |
Order-9 Magic Stars |
General characteristics. Condensed lists of basic solutions
for each of the 3 patterns. |
Order-10 Magic Stars |
General characteristics. Condensed lists of basic solutions
for each of the 3 patterns. |
Order-11 Magic Stars |
General characteristics. Condensed lists of basic solutions
for each of the 4 patterns. |
Prime Magic Stars |
Magic Stars consisting of prime numbers. Lists of minimal
solutions & consecutive primes solutions for orders 5 and 6. |
Prime Magic Stars - 2 |
Diagrams and lists of minimal solutions & consecutive
primes solutions for orders 7 A & B and 8 A & B. |
Unusual magic stars |
Patterns with combinations of stars or more then 4 numbers
per line. |
Iso-like magic stars |
Stars that are transformations of magic squares. Also plusmagic and diammagic squares. |
Trenkler Stars |
Marian Trenkler defines stars as of 2 types. He also defines
almost-magic & weakly-magic |
3-D Magic Stars |
This magic 8-point star contains 12 lines of 3 numbers, plus
many other lines as a result of the missing numbers of the series forming a nucleus and
two satellites. |
Books dealing with Magic Stars |
There are countless examples of individual magic stars
scattered throughout the recreational mathematics literature, but I have only located two
sources containing a serious discussion of this subject. |
Magic Star Puzzles |
Pictures showing star (and
other magic object) puzzles. Some quite old. Also, some pencil-and-paper puzzles of magic objects. |
Star Updates |
This page, started in March, 2005, will
contain material added to this site or links to sub-pages of such
material. |
Simon Whitechapel |
Emails starting in 2001. Simon presents solutions for pattern A of magic stars from 15 to 100. |
Jon Wharf |
Emails starting in 2003. Jon confirms the
total solution count for all orders and patterns from 6 to11, and provides
the total solution count all order 12 patterns. He also supplies some
solutions for all patterns of orders 13 and 14. |
Andrew Howroyd |
First contacted me in February, 2005. He also
confirms all total solution counts and investigated permutations between
patterns of orders 10 and 11. |
Magic 9 x 5 Stars |
This new page shows 1 solution for each magic constant (S) of 46 to 54 of the 5 numbers in each of 9 lines magic hexagram. Note that most magic star pages on this site deal with only 4 numbers/line. |
![]()
Magic stars are similar to Magic Squares in many ways. The order refers to the number of points in the pattern. A standard magic star always contains 4 numbers in each line and in a pure magic star they consist of the series from 1 to 2n where n is the order of the star.
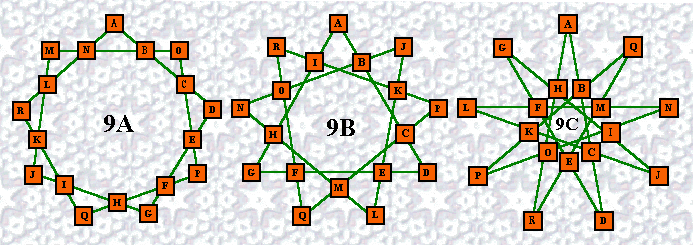
The diagram above demonstrates also how the numbers are assigned to the cells one line
at a time.
Note also, all orders greater then six consist of multiple patterns, each
of which consist of a different list of basic solutions. I have found no reference in the
literature to this fact
Of course, some star patterns have more then two line crossings (plus the two points) per line. See, for example, orders 9b and 9c above. In these cases, we could assign more then 4 numbers to a line in such a way that all lines sum the same. These too would be magic stars. However, to keep the variations to a manageable number, my studies have been limited to the cases where only the perimeter line junctions (i.e. the points and valleys) have numbers assigned to them.
Pattern naming convention. Originally I had rather arbitrarily
assigned names a, b, c, etc to the various patterns of an order of magic star. In January,
2001, Aale de Winkel suggested a systematical way
of applying these labels.
Imagine the points of a star diagram as being points on a circle. Then each point in turn
is connected by a line to another point, by moving around the circle clockwise. If we step
once and connect to the second point, the pattern is called 'A'. Stepping twice, and
connecting to the third point, produces pattern 'B'. etc.
Another way to look at this subject:
'A' has 4 intersections per line, 'B' has 6, 'C' has 8, 'D' has 10, and 'E' (required for
orders 13 and 14) has 12 intersections per line.
By Feb. 16, 2001, all relevant pages have been revised to show the new pattern names.
![]()
Each star has solutions that are apparently different but in fact are only rotations and/or reflections of the basic solution. The order-10 star with its 10 degrees of rotational symmetry, each of which may be reflected, has 20 apparently different solutions. Only one of these is considered the basic solution.
Two characteristics determine the Basic Solution.
Any magic star solution may be converted to a basic solution by normalizing it, i.e. performing the necessary rotations and/or reflections so the solution confirms to the above criteria.
Any magic star can be converted to another magic star by adding or multiplying each
number in the star by a constant. This feature also applies to magic squares.
Of course, the resulting star would not be pure (normal) because the number
series would no longer be consecutive.
![]()
Any magic star can be made into another magic star by complementing each number of the
original star in turn. This is done by subtracting each number from n + 1. In the
case of the order-6 star, which uses the numbers 1 to 12, you subtract each number from 13
to obtain the new number.
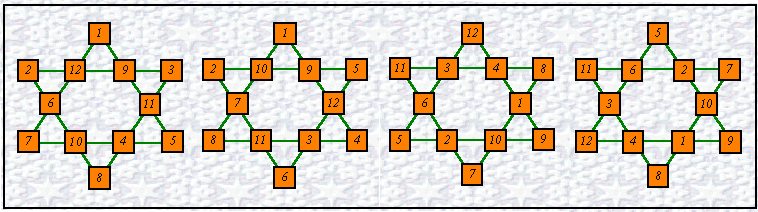 a. # 38
b. # 39
c. complement of # 39 d. normalized c. = # 78
a. # 38
b. # 39
c. complement of # 39 d. normalized c. = # 78
| Diag- ram |
Solut- ion # |
a | b | c | d | e | f | g | h | i | j | k | l | Compl. Sol. # |
Compl. Pair # |
description |
| a. | 38 | 1 | 9 | 11 | 5 | 4 | 10 | 7 | 6 | 12 | 3 | 8 | 2 | 79 | 32 | How solutions are written |
| b. | 39 | 1 | 9 | 12 | 4 | 3 | 11 | 8 | 7 | 10 | 5 | 6 | 2 | 78 | 33 | The next solution in index order |
| c. | 12 | 4 | 1 | 9 | 10 | 2 | 5 | 6 | 3 | 8 | 7 | 11 | Not a basic solution | |||
| d. | 78 | 5 | 2 | 10 | 9 | 1 | 4 | 12 | 3 | 6 | 7 | 8 | 11 | 39 | 33 | Diagram c. normalized by rotation 2 positions clockwise, then a horizontal reflection |
If the original is a basic solution, the complement star will not be a basic solution. It is an equivalent, but after normalizing, it will be another basic solution. When enumerating solutions for magic squares, the complements are also counted as basic solutions. We will follow the same convention when counting and indexing the magic star solutions. This means that the number of solutions for each order of magic star must always be an even number and the number of complement pairs is exactly half the number of total solutions. To put it another way, all basic solutions come in pairs which are complements of each other.
The fact that all solutions have a pair partner determine some characteristics for a particular order. For example, if you find a solution with all odd numbers at the points, you can be confident another solution exists that has all even numbers at the points. Likewise, if a solution exists that has all the low numbers at the points, another one exists that has all the high numbers.
The complementing process works for all magic squares and all magic stars even if the numbers are not consecutive or do not start at 1. In such cases, the complementary number is obtained by subtracting from the sum of the first and last number in the series used. Even prime magic stars have a compliment, although because compliments of many of the prime numbers are not prime numbers, the resulting magic star will not be a prime magic star.
Order-5 magic stars come in pairs where the points of one member appear as the valleys of the other member. I call these pairs Pcomp because they are complements of each other, but not in the accepted sense.
Order-6 is the smallest pure magic star and the only one with only one star pattern (a fact not mentioned in the literature). In fact, in contrast to the voluminous literature for magic squares spanning 100's of years, there has been very little published on magic stars. The two main sources of information I have been able to locate are:
Marián Trenkler of Safarik University,
Kosice, Slovakia published a paper on Magic Stars.
It is called "Magicke hviezdy" (Magic stars) and appeared in Obsory matematiky,
fyziky a informatiky, 51(1998), pages 1-7. (Obsory = horizons (or line of sight)
of mathematics, physics and informatics.
Magic squares, perhaps because they are quite ordered structures, have been studied for centuries. In contrast, magic stars have few similarities between orders, or for that matter even between patterns within an order. This makes it necessary to study each pattern individually
My studies (so far) include all basic solutions for orders 5 to 11 and most solutions
for order-12, a total of 20 patterns.
Also, many solutions for each of the 10 patterns of orders 13 and 14.
![]()
Here are 16 sample magic stars for all orders and
patterns from five to eleven and here are the 14 patterns
for orders twelve to fourteen. And here are 6 examples
of pattern A stars of orders 15 to 20.
Also, be sure to check out Definitions
and Details, and the Order-6 page. Over time, I intend to add
more pages, covering details of the different orders, and including lists of
solutions. So please check this site periodically.
![]()

![]() Please send me Feedback about my Web site!
Please send me Feedback about my Web site!![]()

![]()
Harvey Heinz harveyheinz@shaw.ca
This page last updated
October 31, 2009
Copyright © 1998,1999, 2000 by Harvey D. Heinz