Big Magic Stars

Contents

Introduction

All of the normal magic stars (from orders 6 to 14) on these pages have been found by a computer search. Unlike magic squares, with their regular pattern of an orthogonal array, magic stars have a different pattern for each order and, in fact, multiple patterns within each order. To find solutions for magic stars with these different patterns would require a separate algorithm for each.

I have developed a search algorithm which requires only modest program alterations to adapt to each different pattern. Using an exhaustive search routine has the added advantage that the solutions may be placed in an ordered list.

However, with increased order size, comes increasing work to adapt the program, and increasing search time to find solutions. For this reason, I have not yet tackled orders greater then 14.

On June 26, 2001, Simon Whitechapel sent me an e-mail with a link to a Web site he published. It contains 6  magic stars, one each of orders 15 to 20. They are all of pattern A and all were found by him using a Pascal program.

I show 6 new solutions on this page. All are obtained from his solutions by complimenting and then normalizing .
See my http://www.geocities.com/~harveyh/magicstar.htm page for more information on these steps.

I then show the other possible patterns for each order. They appear in blank form, and await the discovery of solutions.

Six Solutions - Orders 15 - 20

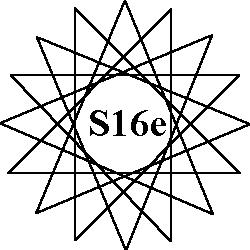
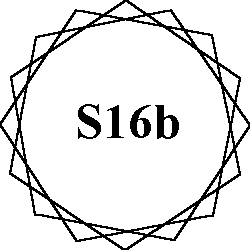
Order-15 pattern A	Order-16 pattern A
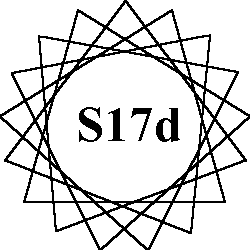
Order-17 pattern A	Order-18 pattern A
Order-19 pattern A	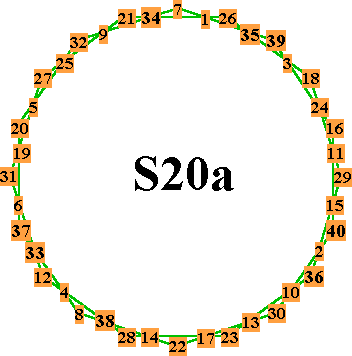Order-20 pattern A

Other Patterns - Order 15

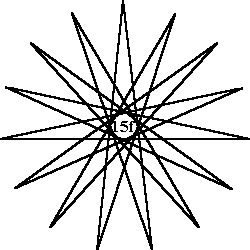		Order- 15 uses numbers from 1 to 30. S = 62. Types of patterns: A = continuous B = 3 pentagons C = continuous D = 5 triangles E = 3 pentagrams F = continuous All orders have at least 1 continuous pattern.

Other Patterns - Order 16

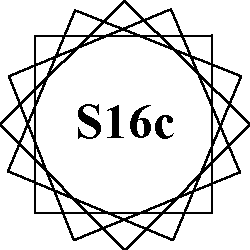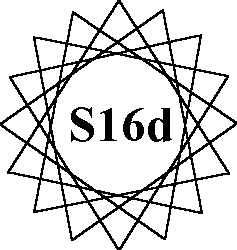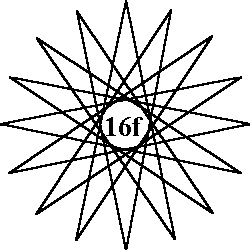		Order- 16 uses numbers from 1 to 32. S = 66. Types of patterns: A = 2 octagons B = continuous C = 4 squares D = continuous E = 2 - 8b stars F = continuous

Other Patterns - Order 17

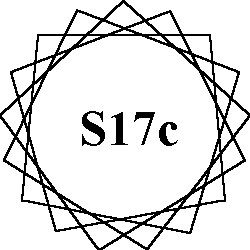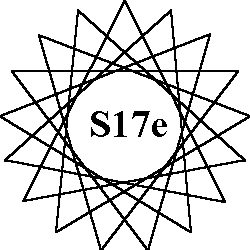
The 7 order-17 patterns of normal magic stars all use the numbers from 1 to 34.
Each of the 17 lines sum to the magic constant of 70.
Because 17 is a prime number, all 7 patterns are continuous (they may be drawn without lifting pen from paper).

Other Patterns - Order 18

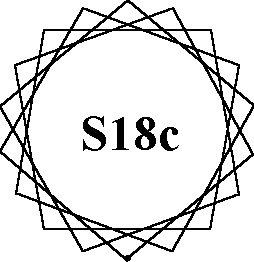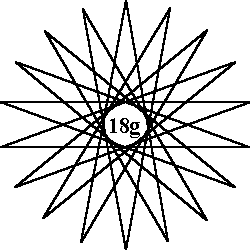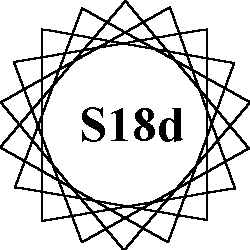
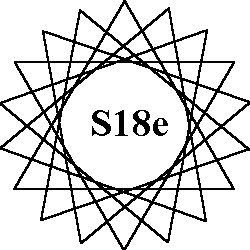
The 7 order-18 patterns of normal magic stars all use the numbers from 1 to 36.
Each of the 18 lines sum to the magic constant of 74.

Types of patterns: A = 2 - 9 sided figures (enneagons), B = 3 hexagons, C = 2 - 9a stars, E = 6 triangles, G= 2 - 9c stars, D & F = continuous.

Other Patterns - Order 19

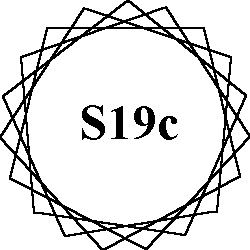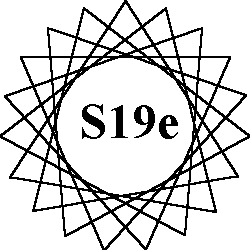	The 8 order-19 patterns of normal magic stars all use the numbers from 1 to 38. Each of the 19 lines sum to the magic constant of 78. Because 19 is a prime number, all 8 patterns are continuous.	Normal magic stars ( a review) All normal magic stars **  use the numbers from 1 to 2n **  have 4 numbers per line and placed at the       exterior points of intersection ** the lowest of all point numbers is at the top      point ** the number at the valley position to the      right of the top point is lower value then the     one in the valley to the left (of the top point)

Other Patterns - Order 20

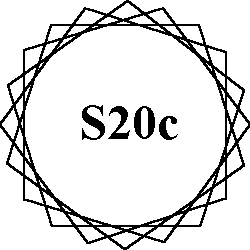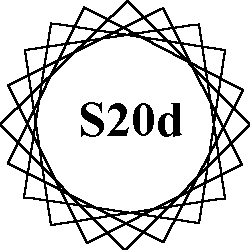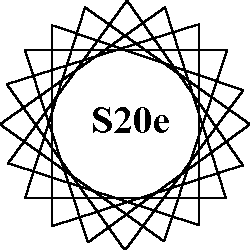
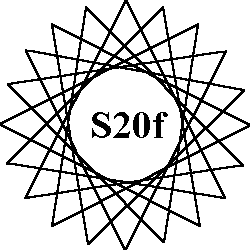
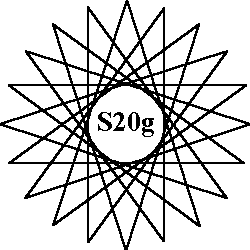
	The 8 order-20 patterns of normal magic stars all use the numbers from 1 to 40. Each of the 20 lines sum to the magic constant of 82. Each pattern has 40 aspects due to rotations and reflections. Use your imagination to guess at the number of apparently different   solutions.(Order- 12b has 826,112 solutions & order-14 an estimated 7,000,000+ basic solutions.)	Description of order-20 patterns. A = 2 decagons B = continuous C = 4 pentagons D = 5 squares E = 2 - 10 point star b patterns F = continuous G = 4 pentagrams H = continuous

Conclusion & a challenge

From the forgoing, it is obvious that there are multiple patterns per order and the number of patterns increase by one for each new odd order.

Notice that pattern 'A' has 4 intersections per line, 'B' has 6, 'C' has 8, 'D' has 10, and 'E'  has 12, 'F' has 14, 'G' has 16, and 'H'  has 18 intersections per line. For a normal magic star, the numbers are always placed on the two outside intersections of the lines.
By patterns F, G, and H, it is getting quite hard to count the number of intersections per line. Of course, to actually write the numbers for a solution onto the pattern, it would have to be enlarged quite significantly.

The challenge!        I welcome, and will acknowledge, all solutions submitted for these patterns.

More solutions:
On Sept. 9, 2003, Simon sent me a text file listing solutions for pattern A for all orders from 15 to 50.
You may download the 29 kb file, Stars.txt

This is the last solution on the file. Anyone wish to draw a diagram for this huge star?

Data for a 50-v magic star (magic total = 202).
(99,100,1, 2), ( 6, 1,97,98), ( 2,97, 7,96), (98, 7, 3,94), (96, 3,95, 8), (94,95, 9, 4), ( 8, 9,93,92),
( 4,93,14,91),(92,14,86,10), (91,86,20, 5), (10,20,87,85), ( 5,87,89,21), (85,89,11,17), (21,11,88,82),
(17,88,84,13), (82,84,24,12), (13,24,90,75), (12,90,81,19), (75,81,31,15), (19,31,78,74), (15,78,83,26),
(74,83,29,16), (26,29,76,71), (16,76,80,30), (71,80,33,18), (30,33,70,69), (18,70,79,35), (69,79,22,32),
(35,22,72,73), (32,72,64,34), (73,64,23,42), (34,23,68,77), (42,68,25,67), (77,25,63,37), (67,63,45,27),
(37,45,61,59), (27,61,48,66), (59,48,38,57), (66,38,40,58), (57,40,43,62), (58,43,49,52), (62,49,41,50),
(52,41,55,54), (50,55,51,46), (54,51,44,53), (46,44,65,47), (53,65,56,28), (47,56,39,60), (28,39,36,99),
(60,36,100,6).
Outer numbers=
99, 6, 2,98,96,94, 8, 4,92,91, 10, 5,85,21,17,82,13,12,75,19,
15,74,26,16,71,30,18,69,35,32, 73,34,42,77,67,37,27,59,66,57,
58,62,52,50,54,46,53,47,28,60.

Inner numbers=
100, 1,97, 7, 3,95, 9,93,14,86, 20,87,89,11,88,84,24,90,81,31,
78,83,29,76,80,33,70,79,22,72, 64,23,68,25,63,45,61,48,38,40,
43,49,41,55,51,44,65,56,39,36.

Good work, Simon!

Please send me Feedback about my Web site!

Last updated May 19, 2007
Harvey Heinz  harveyheinz@shaw.ca
Copyright © 2001 by Harvey D. Heinz