Order-5 Magic Stars

Introduction to Order-5	Cell designations & some of the features of Order-5 magic squares.
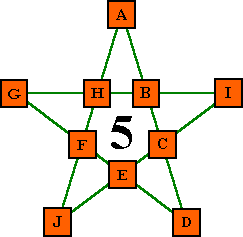
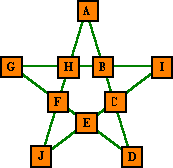
Definitions	Review magic star definitions and general features. Use Back button to return.
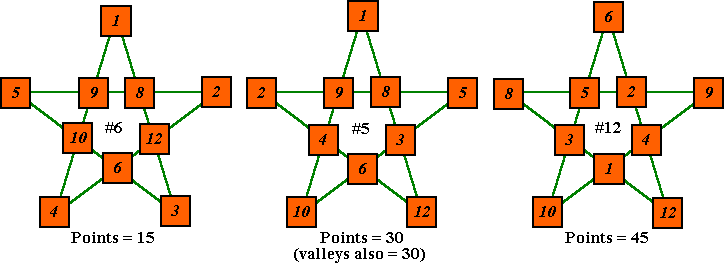
Some examples	Three patterns with points summing to 15, 30 and 45.
A Second series	Order-5 magic star uses the numbers from 1 to 12 with 7 and 11 or 2 and 6 not used. i.e. it is not a pure magic star. The magic constant is 24 or 28 respectively.
Partner Solutions	Equivalent to complement pairs, but for series of non-consecutive numbers.
Point Totals	The 12 point totals in each series form a pattern.
Basic Solutions	The 12 basic solutions with S = 24. Also 12 basic solutions for S = 28.
Relationship to tree-planting problems	A magic star pattern is basically a graph in the form of a polygram. It consists of lines and has numbers at the nodes. Here are the other 5 patterns with 10 numbers in 10 lines of 4.
Almost Magic	Pentagrams with numbers 1 to 10, have only four lines correct (Trigg), or generalized for all orders (Trenkler).
Anti-Magic Pentagrams	The opposite to Magic Stars. These have every line sum different.

Introduction to Order-5

The 5-point star, often referred to as a pentagram is normally included in a selection of magic stars. However, it is not a pure magic star because it cannot be formed with the ten numbers from 1 to 10. The lowest one possible is composed of the numbers from 1 to 12 with 7 and 11 omitted. The magic Sum (S) is 24.

The minimal series

There are 12 basic solutions with S=24 and using series 1 to 12 with 7 and 11 omitted. Each solution has four rotations and five reflections, making a total of 120 variations. The complements of these solutions are solutions of another series with S = 28.

The point totals vary from 15 to 45 with one solution having the points summing to 24, the constant S.

Some examples

A Second Series

Another set of 12 solutions is obtainable from the same series of 1 to 12, but leaving out the 2 and 6. The constant (S) for this series is (70/2) * 5 = 28. As mentioned above, all solutions of this set are compliments of the 12 solutions of the first set where S = 24.

Series with 1 and 7 missing or 3 and 5 missing also sum to 70 but no solutions exist.
The series from 1 to 11 with 6 missing gives a sum of 60, permitting S = 24, but no solutions exist.

S = 2/5 of the sum of the series, so regardless of what series is used, S must be an even
number. Any S (greater then 24) may be obtained by modifying a basic solution in the following manner:

add 1 to each point or valley will give an S of 26
add 2 to each point or valley will give an S of 28
add 1 to each point and valley will give an S of 28
etc.

Partner Solutions (pcomp pairs)

Any solution for S = 24 may be converted to a partner solution by the following algorithm, which moves the points to the valleys and the valleys to the points.

                     a and e exchange places
                     b moves to i, c moves to j, d moves to c, f moves to d
                     g moves to b, h moves to g, i moves to h, j moves to f

The resulting solution, while equivalent, will however, be a rotation and/or a reflection of the basic solution.
The six pairs of solutions are: #1 and #8, #2 and # 7 ( no rotation or reflection required), # 3 and #9, # 4 and #11, # 5 and # 10, # 6 and # 12.

Point Totals

Point totals for minimal series (no 7 and 11):
15  21  24  27  30  33  36  39  45
            27  30  33             Note that all are mod 3 = 0
Point totals with no 2 and 6:
20  26  29  32  35  38  41  44  50
            32  35  38             Note that all are mod 3 = 2

As 30 and 35, the middle number in each series of totals, are each one-half of the respective series sums, the valleys in each case also sum to 30 and 35 respectively.

Minimal Basic Solutions for Order-5 S = 24

                                             Point  pcomp
 #   A   b   c   D   e   f   G   h   I   J   Point  pair #   Remarks
 1   1   3   8  12   2   4   6  10   5   9    33    1       
 2   1   3  12   8   2   9   5  10   6   4    24    2  Points are magic!
 3   1   4   9  10   5   3   6  12   2   8    27    3   
 4   1   4  10   9   5   8   2  12   6   3    21    4   
 5   1   8   3  12   6   4   2   9   5  10    30    5  Valleys also 30
 6   1   8  12   3   6  10   5   9   2   4    15    6  Points are lowest #'s
 7   2   5   8   9   1   4  10   6   3  12    36    2   
 8   2   5   9   8   1  12   3   6  10   4    27    1   
 9   3   1   8  12   2   6   4  10   9   5    33    3   
10   3   1  12   8   2   5   9  10   4   6    30    5  Valleys also 30
11   4   2   6  12   3   1   8   9   5  10    39    4   
12   6   2   4  12   1   3   8   5   9  10    45    6  Points are highest #'s

Basic Solutions for Order-5 S = 28

                                             Point  pcomp
 #   A   b   c   D   e   f   G   h   I   J   Point  pair #   Remarks
 1   1   5  10  12   3   9   4  11   8   7    32    1   
 2   1   5  12  10   3   7   8  11   4   9    32    2
 3   1   7   9  11   4   5   8  10   3  12    35    3  Valleys also 35
 4   1   7  11   9   4  12   3  10   8   5    26    4
 5   1   9   7  11   8   5   4  12   3  10    29    5
 6   1   9  11   7   8  10   3  12   4   5    20    6  Pts.are lowest numbers
 7   3   4   9  12   1  10   5   8  11   7    38    2
 8   3   4  12   9   1   7  11   8   5  10    38    1
 9   4   3   9  12   1   5  10   8   7  11    44    4
10   4   3  12   9   1  11   7   8  10   5    35    3  Valleys also 35
11   5   1  10  12   3   4   9  11   7   8    41    5
12   8   3   7  10   1   5  12   4   9  11    50    6  Points are highest #'s

The solutions of the second series are complements (after normalizing) of 
solutions in the first series.

Relationship to tree-planting problems

A popular classification of recreational mathematics problems are know as tree-planting problems. The problem specifies how many trees, how many trees per row, and how many rows. This illustration shows the six basic patterns for 10 objects in 5 rows of 4, using numbers instead of trees. In each case, the hypothetical trees have been replaced with 10 of the first 12 integers (there are no solutions using the numbers 1 to 10).

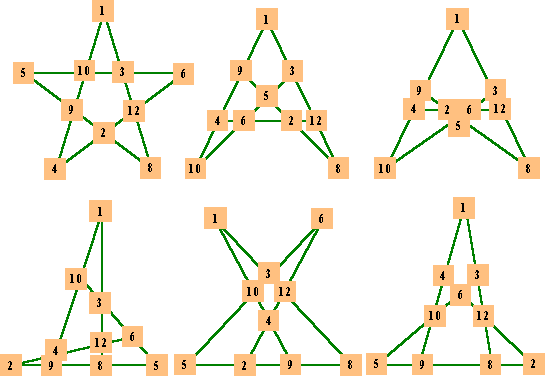
Order5-3.gif (8359 bytes)

The first pattern is the magic 5-pointed star, the other five maintain the arrangement of numbers so each line sums correctly.

In each case the 7 and 11 are not used. The sum per line is 24. If we omit the 2 and the 6 instead of the 7 and 11, the sum per line is 28. In both cases, there are 12 basic solutions.

Almost Magic Pentagrams

A magic pentagram, we now know, must have 5 lines summing to an equal value.

Charles Trigg (see reference) calls a pentagram with only 4 equal lines but constructed with the consecutive numbers from 1 to 10, an almost magic pentagram.

The numbers from 1 to 10 sum to 55, and as each appears in two lines the total for the five lines is 110. If we assume only 4 lines are correct, then 4x + y = 110.

There are six solutions to this equation. (x,y) = (25, 10), (24, 14), (23, 18), (21, 26), (20, 30), (and (19, 34). These form into 3 complement pairs, and it turns out only two of the pairs can form valid solutions.

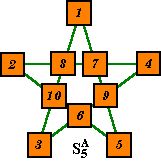
There are seven basic solutions as shown here. The numbers are placed in the corresponding standard positions shown above.

 A    B    C    D    E    F    G    H    I    J     X    Y
 8    2    3    1   10    4    9    7    6    5     24   14
 7    2    4    1    5    8   10    3    9    6     24   14
10    2    5    1    7    6    9    4    8    3     27   18
 9    2    6    1    5    7   10    3    8    4     27   18
10    3    4    1    9    6    7    5    8    2     27   18
 7    4    6    1   10    3    9    8    2    5     27   18
 4    3    9    2    6   10    5    8    7    1     27   18

In each case, the numbers at a, b, c, d form the first line, which is line y.

The complement of each solution is obtained by subtracting each number in turn from 11.

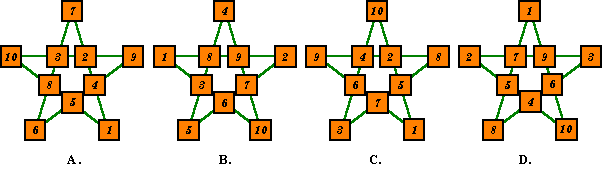
Almost-2.gif (5279 bytes)

A. is solution number 2 (from the above table) x = 24, y = 14
B. is the complement of A x = 20, y = 30
C. is solution number 3 (from the above table) x = 23, y = 18
D. is the complement of C x = 21, y = 26

Each of the seven basic solutions above, and their complement solutions can be changed into another eleven solutions by performing the following transformation (on the basic solution).

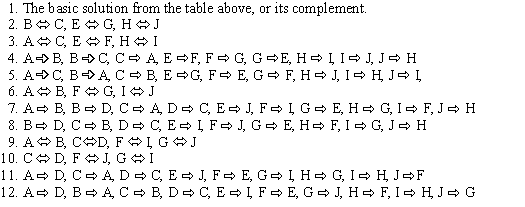
Almost-3.gif (5301 bytes)

Therefore, there are 7 x 2 x 12 = 168 solutions without counting rotations or reflections.
In each case, line y is the first line of the pattern.

See Charles W. Trigg, Almost Magic Pentagrams, Journal of Recreational Mathematics 29:1, p. 8-11, 1998, for more information.

Footnote: Trenkler almost-magic stars

Marián Trenkler (see Trenkler Stars) has independently coined the phrase almost-magic, but generalizes it for all orders of stars.

His definition:
If there are numbers 1, 2, …, 2n located in a star S_n ( or T_n) so that the sum on n – 2 lines is 4n + 2, on the others 4n + 1 and 4n + 3, we call it an almost-magic star.

NOTE that by his definition, the order-5 almost-magic star has only 3 lines summing correctly. Trigg’s order-5 (the only order he defines) has 4 lines summing the same.

Anti-Magic Pentagrams

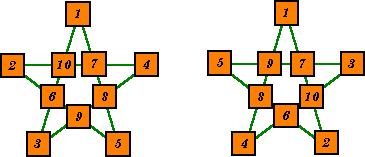Anti-magic pentagrams are order-5 stars using the consecutive numbers from 1 to 10. Each of the five lines must sum to a different value.

Here we show two of many such arrangements. In both these cases the line sums are consecutive.

Charles Trigg (1) reported that there are 2208 distinct solutions with consecutive line sums for the order 5 anti-magic pentagram.

(1) Charles Trigg Journal of Recreational Mathematics, vol.10(3), 1977-78

Please send me Feedback about my Web site!