 |
 |
 |
 |
 |
Magic Star - Defined |
What is a magic star and a method to determine the basic solutions |
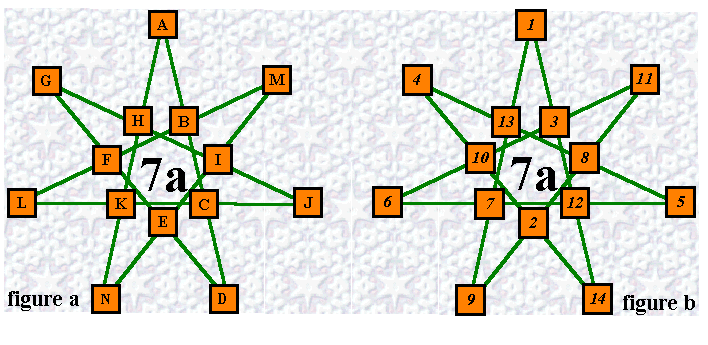
Star Definition Illustrated |
An Order-7a magic star illustrates points of the definition |
To support my definition |
No other definition, no mention of multiple patterns, it's needed |
Trenkler Stars |
There are two types of 4-numbers-in-a-row stars |
Value of Magic Sum |
Equation for determining the magic sum or constant for any order |
Multiple Patterns per Order |
All orders greater then six have multiple ways of drawing the star |
Points, patterns & total solutions |
This table shows the point names, type of pattern and total number of solutions. Also shown is the time required to compile each list. |
Number of Basic Solutions |
As the Order number increases, so does the number of basic solutions (except order-7). Some notes and common characteristics. |
A Practical Example |
See my Primestars page for an actual situation where three different definitions were used (a competition to find order-5 prime stars). |
The pattern for Order-7a is shown below to help illustrate the definition.
Each of the 20 patterns from Order-5 to Order-12d may be seen at magic star examples.
As a prerequisite to a comprehensive study of Magic Stars. the first requirement is a formal definition. As I have not been able to find one in the literature, this is the definition I propose.
Definition
A pure magic star is a set of integers 1, 2, 3, ...,
2n which are placed at the 2n exterior points of intersection of the lines which
form a regular polygram, such that the sum of the four integers found in any of the n lines
is given by: S = 4n+2 where S is called the magic sum,
and n is the order of the star.
NOTES:
NOTES regarding the above points
Traditionally, cell designations have been shown row by row from top down and reading from left to right.. I have chosen to show them starting from the top but reading along each line in order
![]()
I apologize to the hobbyists out there who have compiled lists of solutions using the row by row method, but as I started investigating the higher orders found that method simply to awkward and open to error. However, for orders 6 and 7, I have converted several of these lists to my system and found they compare perfectly so everyone seems to be coming up with the same results. My hope is that this definition will become a standard so that we can all compare our findings to the mutual benefit of the subject.
![]()
Marián Trenkler has published a paper on magic stars in which he has defined magic stars with four numbers per line as type S or type T.
The stars I am mainly concerned with on this site (and have defined above), are Type S.
Type T stars differ in that the numbers that here appear in the valleys are located at intersections in the interior of the star.
His paper also defines;
Weakly-magic stars as those constructed from number sets that are
not consecutive.
Almost-magic stars as those using consecutive numbers but have n
– 2 lines summing to 4n + 2, and the others sum to 4n + 1 and 4n
+ 3.
An order-5 magic star with 10 numbers from 1 to 12 is a weakly-magic star.
An order-5 magic star using numbers 1 to 10 is an almost-magic star.
For more details and examples go to Trenkler.htm (on this site)
In magic star patterns, each number appears in two lines so the formula to calculate the magic constant is:
S = Sum of the series / number of points * 2
For the 5-point magic star the sum of 1 to 12 = 78 less 7 and 11 = 60 so 60/5 * 2 = 24.
For the 6-point magic star the sum of 1 to 12 = 78 so 78/6 * 2 = 26
For the 7-point star the sum of 1 to 14 = 105 so 105/7 * 2 = 30, etc...
In general, when n is the order, S = 4n + 2.
What do I mean by pattern?
I have been using the word pattern ambiguously to refer to an arrangement of numbers that compose a magic star, and also to the arrangement of lines that together form the diagram of a star. It is this second definition I wish to discuss at this time.
The order-6 magic star can be formed with only one pattern of lines. However, from order-7 upwards, there are at least 2 patterns possible for each order. My magic star definition limits the position of the cells (numbers) to four per line and at the peaks and valleys only, or there would be many more patterns possible.
Even though the patterns change completely from order to order, there is a surprisingly similar correspondence of peaks. Or, because every fourth designation as we trace through the pattern is a peak, maybe not surprising. The list below illustrates this similarity. Note that one point of the two patterns of order-8 differs, yet the number of solutions is the same. With all the other orders, if the points are similar, the number of solutions is the same, if they differ the solution total differs also.When we get to Order-11, though, there are two solutions (a & c) that differ from the pair with similar point names. They also differ from each other, but the number of solutions is the same (just as order-8). Presumably the same will apply to Order-12, but so far I have a complete solution list only for 12b.
5 a d g i j not a pure magic star 12 Continuous 11 seconds 6 a d g j k l 80 2 triangles 7 seconds 7a a d g j l m n 72 Continuous 1.4 minutes 7b a d g j l m n 72 Continuous 1.1 minutes 8a a d g j m n o p 112 2 squares 1.1 minutes 8b a d g I m n o p 112 Continuous 4.7 minutes 9a a d g j m o p q r 3014 Continuous 2.21 hours 9b a d g j l n p q r 1676 3 triangles 18 minutes 9c a d g j l n p q r 1676 Continuous 19.3 minutes 10a a d g j m p q r s t 10882 2 pentagons 24 hours 10b a d g j m o q r s t 115552 Continuous 6.5 hours 10c a d g j m p q r s t 10882 2 pentagrams 24 hours 11a a d g j m p r s t u v 53528 Continuous 62 days 11b a d g j l n p r t u v 75940 Continuous 33.6 hours 11c a d g i k m o q s u v 53528 Continuous 5.3 hours 11d a d g j l n p r t u v 75940 Continuous 20.2 hours 12a a d g j m p s t u v w x >800000 2 hexagons to assign the 12b a d g j m o q s u v w x 826112 3 squares 39.5 days (+ 46 days 12c a d g j l n p r t v w x >800000 4 triangles complement pairs) 12d a d g j m o q s u v w x 826112? Continuous 13a a d g j m p s u v w x y z >3,000,000 Continuous 13b a d g j m p s u v w x y z >3,000,000 Continuous 13c a d g j m p r t v w x y z >3,000,000 Continuous 13d a d g j m o q s u w x y z >3,000,000 Continuous 13e a d g j l n p r t v x y z >3,000,000 Continuous 14a a d g i k m o q s u w y aa bb >7,000,000 Continuous 14b a d g j m o q s u w y z aa bb >7,000,000 Continuous 14c a d g j m p s v w x y z aa bb >7,000,000 2 heptagons 14d a d g j m p s v w x y z aa bb >7,000,000 2 7-point star-b pattern 14e a d g j m p s v w x y z aa bb >7,000,000 2 7-point star-a pattern
The orders are in pairs, with an odd and the next even order having the same number of
patterns.
If two patterns have the same point names, the number of basic solutions is the same and
the value and the value of cell a changes at the same solution
number (except for order-9).
I have included patterns for Order-13 and Order-14 as a point of interest. However, it will probably be sometime in the future before these ten complete lists of solutions will be found. At this time, personal computers are simply not fast enough to explore the large number of permutations.
The last column (above) indicates the length of time required to search for all the
basic solutions for each pattern. The computer used is a 200 Mhz Pentium II with 32 Megs
of RAM. The program is written in QuickBasic, then compiled and run in a DOS window.
The number of consecutive letters as the final cell names is an indication of relative
running time. For example, 11a has five consecutive letters at the end
and took 62 days to run; 11c has only two and took 5.3 hours.
| March 1, 2005 update: I have posted some new pages on this site. Both Jon Wharf and Andrew Howroyd have confirmed all my solution totals for orders 5 to 11 using much faster programs. Andrew has also found all solutions for the 4 order 12 patterns. They are 12a: 396,930 (29 sec.); 12b: 826,112 (16 min.); 12c: 560,348 (7 min..) ; 12d: 496,336 (6 min.). |
![]()
Pattern naming convention. Originally I had rather arbitrarily
assigned names a, b, c, etc to the various patterns of an order of magic star. In January,
2001, Aale de Winkel suggested a systematical way
of applying these labels.
Imagine the points of a star diagram as being points on a circle. Then each point in turn
is connected by a line to another point, by moving around the circle clockwise. If we step
once and connect to the second point, the pattern is called 'A'. Stepping twice, and
connecting to the third point, produces pattern 'B'. etc.
Another way to look at this subject:
'A' has 4 intersections per line, 'B' has 6, 'C' has 8, 'D' has 10, and 'E' (required for
orders 13 and 14) has 12 intersections per line.
By Feb. 16, 2001, all relevant pages have been revised to show the new pattern names.
With increasing order, and a corresponding increase in the length of the series, the complexity of the pattern goes up as is to be expected. We would expect the number of basic solutions to also go up. And so they do (I’ve tested to order-12), except for the case of order-7 which has less solutions then order-6.
Another exception to the increasing number of solutions is order-11, where all 4 patterns have less solutions then Order-10b. Is it coincidence that in both cases, it is the first occurrence of two patterns with the same number of solutions? (In the case of Order-11, this is a second pair.)
The number of solutions for each order is always an even number because each basic solution has a complement, which, after normalizing, is also a basic solution. Another way to say this is that all basic solutions come in pairs that are complements of each other.
Orders 6, 8 and 10 do not have solutions with all low numbers at the points and therefor also do not have solutions with all high numbers at the points (because of complements). All other orders do have such solutions, including order-12, thus ending speculation that this is a feature of even orders.
Order-5 has been included in this study for comparison purposes although it is not a
pure magic star.
With this one exception this study is limited to pure magic stars only.
Lists are of basic solutions only. Each order has 2n-1 disguised versions. So order-14
with over 7 million basic solutions has over 196 million apparently different solutions.
Because of the large file sizes for order-9 and higher, I include condensed lists only,
showing some solutions at the start and end, and when the value of cell a changes.
![]()

![]() Please send me Feedback about my Web site!
Please send me Feedback about my Web site!![]()

![]()
![]()
Harvey Heinz harveyheinz@shaw.ca
This page last updated
March 11, 2006
Copyright © 1998, 1999, 2000 by Harvey D. Heinz