Prime Magic Stars-2

But_Sqrs.gif (5472 bytes) Aro_up.gif (318 bytes) Home.gif (5413 bytes) But_Strs.gif (1861 bytes) But_Patt.gif (1837 bytes)

Welcome to magic stars formed with prime numbers

Order-7 minimal solution

 All basic solutions for minimum sum prime number magic stars.

Order-7 consecutive primes

 All basic solutions for consecutive prime number magic stars.

Order-8 minimal solution

 All basic solutions for minimum sum prime number magic stars.

Order-8 consecutive primes

 All basic solutions for consecutive prime number magic stars.

Introduction

This page deals with orders 7 and 8 prime magic stars. A preceding page, Prime Magic Stars, shows prime star solutions for orders 5 and 6.

There are two types of solutions to consider.
    The solution with the lowest magic constant but with missing primes in the number set used.
    The solution using the smallest set of consecutive prime numbers.
In each case there will be multiple solutions (usually) obtained from the same set of prime numbers.

Because we are concerned on this page with 2 orders (7 and 8), and there are 2 patterns per order, there are a total of 8 sets of solutions. Note that only the basic solutions are presented here. Each has 14 aspects for order-7 and 16 aspects for order-8. Refer to my Magic Stars Definitions page for an explanation.

Notice that in all cases, if a set of prime numbers produce solutions for  pattern A or B, it will also produce solutions for the other pattern. However, the number of solutions for each pattern may not be identical.

These solutions were obtained by an exhaustive computer search. With an investigation based only on searching, there is always the danger that a mistake exists in the search algorithm, resulting in some solutions being missed.
I can only say that my algorithm has been proved accurate for finding the normal basic solutions for orders 5, 6, 7 and 8 and for the solutions for prime magic stars of order-5, as confirmed by other researchers.
I am most happy to hear from anyone obtaining results differing from those presented here.

    rule-w.gif (2718 bytes)

The Minimal Solution Order-7 Prime Magic Star, Pattern A

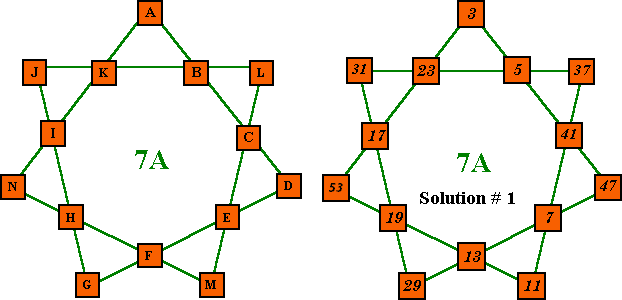
p7a_min-1.gif (7088 bytes)

Minimal solutions, pattern 7A

In this table of solutions, "Pk" and "Val" columns show the totals for the peaks and the valleys. The totals in bold are prime numbers. The "Remarks" column indicates the prime number(s) missing from the sequence of primes used.
Shown are all the basic solutions with magic sums of 96 (the minimum possible) or 100.

# A b c D e f G h i J k L M N Sum Pk Val Remarks - Pattern 7A
1 3 5 41 47 7 13 29 19 17 31 23 37 11 53 96 211 125 Primes 3 to 53. No # 43
2 3 5 47 41 7 19 29 13 17 37 23 31 11 53 96 205 131
3 3 11 53 29 17 13 37 23 5 31 47 7 19 41 96 167 169
4 7 3 19 71 13 5 11 17 29 43 23 31 37 41 100 241 109 Primes 3 to 71.
No # 47, 53, 59, 61, 67
5 3 19 17 61 11 23 5 29 53 13 37 31 41 7 100 161 189 3 to 61. No 43, 47, 59
6 5 13 53 29 23 11 37 41 3 19 61 7 17 31 100 145 205
7 19 13 7 61 3 5 31 17 29 23 11 53 37 41 100 246 107
8 7 3 37 53 13 5 29 17 11 43 23 31 19 59 100 241 109 3 to 59.  No # 41, 47
9 3 7 29 61 5 23 11 17 41 31 43 19 47 13 100 185 165 3 to 61. No # 37, 53, 59
10 3 19 17 61 5 11 23 29 41 7 43 31 47 13 100 185 165
11 3 19 17 61 23 11 5 47 41 7 43 31 29 13 100 149 201
12 7 3 29 61 11 5 23 17 19 41 43 13 47 31 100 223 127

rule-n.gif (1968 bytes)

The Minimal Solution Order-7 Prime Magic Star, Pattern B

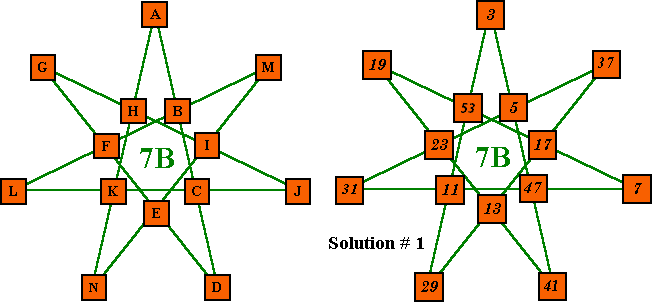
p7b_min-1.gif (7789 bytes)

 

Minimal solutions, pattern 7B

In this table of minimum solutions, "Pk" and "Val" columns show the totals for the peaks and the valleys. The totals in bold are prime numbers. The "Remarks" column indicates the prime number(s) missing from the sequence of primes used.
Shown are all the basic solutions with magic sums of 96 (the minimum possible) or 100.
Notice that there are 13 solutions for pattern 7B but only 12 for 7A.

# A b c D e f G h i J k L M N Sum Pk Val Remarks - Pat. 7B
1 3 5 47 41 13 23 19 53 17 7 11 31 37 29 96 167 169 Primes 3 to 53. No 43
2 3 17 23 53 13 19 11 41 7 37 5 31 29 47 96 211 125
3 3 17 23 53 19 13 11 47 7 31 5 37 29 41 96 205 131
4 7 19 3 71 5 13 11 29 17 43 23 31 37 41 100 241 109 Primes 3 to 71.
No 47, 53, 59, 61
5 3 17 19 61 23 11 5 53 29 13 37 31 41 7 100 161 189 3 to 61. No 43, 47, 59
6 5 3 61 31 11 41 17 53 23 7 13 19 37 29 100 145 205
7 19 7 13 61 5 3 31 29 17 23 11 53 37 41 100 246 104
8 7 11 23 59 5 17 19 37 13 31 3 43 29 53 100 241 109 3 to 59. No 41, 47
9 7 29 5 59 17 11 13 31 3 53 19 23 37 43 100 235 105
10 3 17 19 61 11 5 23 41 29 7 43 31 47 13 100 185 165 3 to 61. No 37, 53, 59
11 3 17 19 61 11 23 5 41 47 7 43 31 29 13 100 149 201
12 3 29 7 61 23 5 11 41 17 31 43 19 47 13 100 185 165
13 7 19 43 31 5 17 47 29 11 13 3 41 23 61 100 223 127

With these small primes, a relatively large percentage of peak and valley totals are prime. However, with the slightly higher prime numbers in the consecutive series, the totals that are prime are a much smaller percentage. And of course, for order-8, no peak or valley totals can be prime, because all these totals must be even numbers.

Peaks and valley totals that are prime.
  # of Solutions Peaks Valleys
Minimal sum - Pattern A 12 6 4
Pattern B 13 6 4
Consecutive sum - Pattern A 10 0 2
Pattern B 14 0 2

Top.gif (1256 bytes)

rule-w.gif (2718 bytes)

Order-7A  using consecutive primes

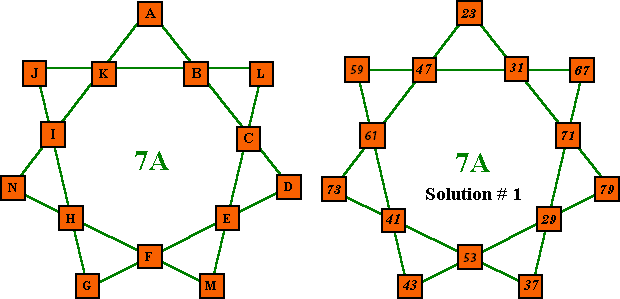
p7a_con-1.gif (7042 bytes)

Consecutive primes, pattern 7A

In these consecutive primes table of solutions, I have chosen not to include the "Pk" and "Val" columns because, of a total of 24 solutions, no peak totals are prime and only 4 valley totals.  Notice that there are 10 pattern A solutions and 14 pattern B solutions in these 3 sets of consecutive primes. These are all the basic solutions possible for series of 14 consecutive prime numbers starting with 23, 307 and 409.

# A b c D e f G h i J k L M N Sum Primes used
1 23 31 71 79 29 53 43 41 61 59 47 67 37 73 204 23 to 79
2 23 31 71 79 37 59 29 61 67 47 73 53 43 41 204
3 23 37 71 73 31 53 47 67 61 29 79 59 43 41 204
4 23 41 67 73 29 31 71 53 43 37 79 47 61 59 204
5 23 41 67 73 29 59 43 53 71 37 79 47 61 31 204
6 29 23 79 73 41 43 47 59 37 61 67 53 31 71 204
7 29 43 59 73 61 23 47 79 37 41 67 53 31 71 204
8 317 337 401 397 347 359 349 383 367 353 389 373 331 379 1452 317 to 401
9 449 419 433 487 409 431 461 421 443 463 439 467 479 457 1788 409 to 487
10 449 419 433 487 431 409 461 443 421 463 439 467 45 479 1788

rule-n.gif (1968 bytes)

Order-7B  using consecutive primes

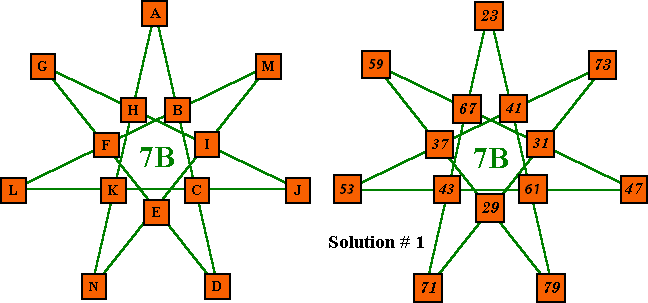
p7b_con-1.gif (8138 bytes)

Consecutive primes, pattern 7B

# A b c D e f G h i J k L M N Sum Primes used
1 23 41 61 79 29 37 59 67 31 47 43 53 73 71 204 23 to 79
2 23 43 79 59 31 53 61 67 29 47 41 37 71 73 204
3 23 61 41 79 53 29 43 71 31 59 37 67 47 73 204
4 23 61 47 73 53 41 37 71 29 67 31 59 43 79 204
5 23 61 79 41 53 67 43 71 31 59 37 29 47 73 204
6 23 67 41 73 59 29 43 71 53 37 79 47 61 31 204
7 23 67 73 41 59 61 43 71 37 53 31 47 29 79 204
8 29 37 67 71 23 79 31 59 61 53 43 41 47 73 204
9 29 37 67 71 43 59 31 79 41 53 23 61 47 73 204
10 317 367 389 379 359 383 331 401 347 373 337 353 349 397 1452 317 to 401
11 317 379 373 383 367 353 349 397 359 347 401 331 389 337 1452
12 409 449 463 467 443 421 457 479 419 433 461 431 487 439 1788 409 to 487
13 449 421 439 479 409 443 457 433 431 467 419 463 461 487 1788
14 449 433 419 487 431 409 461 443 421 463 439 467 479 457 1788

Top.gif (1256 bytes)

rule-w.gif (2718 bytes)

The Minimal Solution Order-8 Prime Magic Star, Pattern A

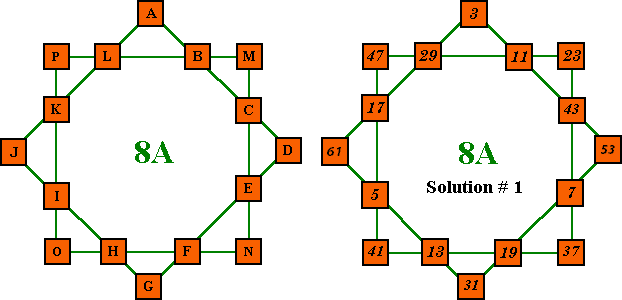
p8a_min-1.gif (7257 bytes)

Minimal solutions, pattern 8A

The "Remarks" column indicates the prime number(s) missing from the sequence of primes used.
Shown are all the basic solutions for order-8A with magic sums of 110 (the minimum possible), 114 or 116.
Notice that there are 16 minimal solutions for pattern 8A and 19 for pattern 8B.

# A b c D e f G h i J k l M N O P Sum Remarks - 8A
1 3 11 43 53 7 19 31 13 5 61 17 29 23 37 41 47 110 3-61. No number 59
2 3 11 43 53 31 19 7 37 5 61 17 29 23 13 41 47 110
3 3 11 43 53 31 19 7 61 5 37 41 29 23 13 17 47 110
4 3 29 17 61 5 13 31 19 7 53 43 11 47 41 37 23 110
5 3 29 17 61 5 37 7 19 31 53 43 11 47 41 13 23 110
6 3 29 41 37 5 7 61 19 13 17 43 47 11 53 31 23 110
7 3 5 47 59 19 13 23 43 37 11 29 71 7 41 17 31 114 3-71. No 53,61,67
8 3 5 47 59 19 13 23 43 37 11 29 71 31 17 41 7 114
9 3 11 29 71 23 13 7 17 31 59 5 47 19 43 41 37 114
10 3 11 71 29 19 43 23 13 31 47 5 59 7 17 41 37 114
11 3 11 71 29 23 43 19 17 31 47 5 59 7 13 41 37 114
12 7 19 31 59 5 29 23 3 11 79 17 13 37 43 41 4 116 Primes 3-79.
No 53,61,67,71,73
13 7 19 31 59 5 29 23 3 11 79 17 13 43 37 47 4 116
14 7 19 31 59 5 41 11 3 23 79 17 13 37 43 29 4 116
15 7 47 3 59 23 5 29 13 43 31 37 41 11 79 19 1 116
16 3 5 41 67 11 7 31 19 37 29 13 71 17 47 43 23 116 3-71. No 51-53-61

rule-n.gif (1968 bytes)

The Minimal Solution Order-8 Prime Magic Star, Pattern B

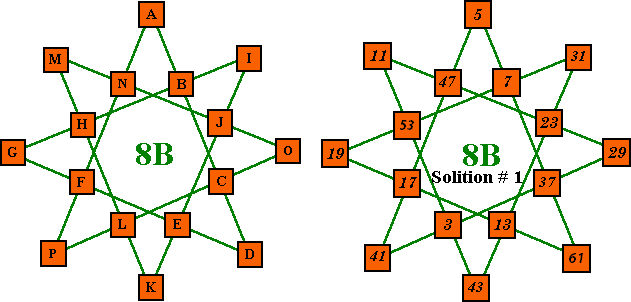
p8b_min-1.gif (8450 bytes)

Minimal solutions, pattern 8B

# A b c D e f G h I j K l M n O P Sum Remarks - 8B
1 5 7 37 61 13 17 19 53 31 23 43 3 11 47 29 41 110 3-61. No number 59
2 5 7 61 37 13 41 19 53 31 23 43 3 11 47 29 17 110
3 5 11 53 41 3 37 29 23 47 17 43 31 13 61 19 7 110
4 5 31 61 13 37 41 19 53 7 23 43 3 11 47 29 17 110
5 19 13 17 61 11 7 31 23 43 3 53 5 29 37 41 47 110
6 5 3 47 59 7 37 11 29 71 13 23 19 43 41 17 31 114 3-71. No 53,61,67
7 5 3 47 59 7 37 11 29 71 17 19 23 43 41 13 31 114
8 5 3 59 47 19 37 11 71 29 43 23 7 13 41 17 31 114
9 5 7 31 71 11 3 29 41 37 23 43 17 13 59 19 47 114
10 5 31 7 71 11 3 29 17 37 23 43 41 13 59 19 47 114
11 23 7 13 71 3 11 29 19 59 5 47 17 31 37 41 43 114
12 3 7 59 47 17 11 41 31 37 19 43 29 13 79 5 23 116 Primes 3-79.
No 53,61,67,71,73
13 3 37 29 47 41 23 5 31 43 13 19 59 7 79 17 11 116
14 3 37 47 29 59 23 5 43 31 7 19 41 13 79 17 11 116
15 3 37 59 17 47 11 41 31 7 19 43 29 13 79 5 23 116
16 3 43 29 41 47 23 5 31 37 13 19 59 7 79 17 11 116
17 3 43 29 41 59 11 5 37 31 7 19 47 13 79 17 23 116
18 3 43 41 29 59 23 5 37 31 7 19 47 13 79 17 11 116
19 5 23 17 71 29 3 13 43 37 31 19 47 7 67 11 41 116 3-71. No 51,53,61

Top.gif (1256 bytes)

rule-w.gif (2726 bytes)

Order-8A using consecutive primes

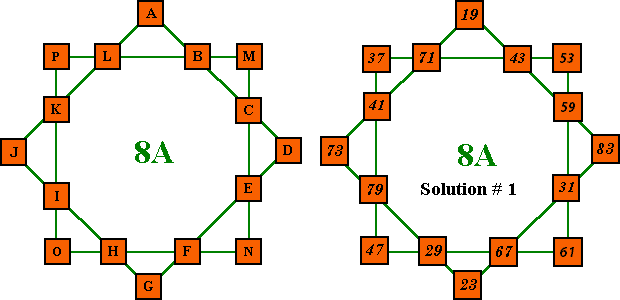
p8a_con-1.gif (7409 bytes)

Consecutive primes solutions, pattern 8A

Here are  solutions for order-8,  using consecutive prime sets 19 - 83 (the minimum possible), 29 - 97, 31 - 101 and 53 - 127.

# A b c D e f G h i J k l M N O P Sum Remarks - 8A
1 19 43 59 83 31 67 23 29 79 73 41 71 53 61 47 37 204 Primes 19 to 83
2 19 47 79 59 41 67 37 23 71 73 29 83 31 53 61 43 204
3 19 53 73 59 29 37 79 23 31 71 47 67 41 61 83 43 204
4 19 67 47 71 31 23 79 37 29 59 73 53 43 83 61 41 204
5 19 67 71 47 37 41 79 29 53 43 59 83 23 73 61 31 204
6 23 19 79 83 43 37 41 71 31 61 47 73 53 29 67 59 204
7 23 19 79 83 43 47 31 61 41 71 37 73 53 29 67 59 204
8 23 19 83 79 43 53 29 61 41 73 37 71 47 31 59 67 204
9 23 37 71 73 19 83 29 43 53 79 61 41 67 47 31 59 204
10 23 37 73 71 19 47 67 43 53 41 61 79 29 83 31 59 204
11 23 73 47 61 19 53 71 29 37 67 83 31 59 79 43 41 204
12 29 47 67 97 31 71 41 43 83 73 59 79 53 89 37 61 240 Primes 29 to 97
13 31 41 89 97 71 47 43 83 59 73 53 101 37 61 67 79 258 Primes 31 to 101
14 31 47 101 79 53 67 59 89 37 73 83 71 43 61 41 97 258
15 31 53 101 73 59 83 43 47 71 97 41 89 37 61 67 79 258
16 31 53 101 73 59 83 43 47 79 89 41 97 37 61 67 71 258
17 31 59 71 97 47 41 73 89 53 43 101 83 79 61 67 37 258
18 53 67 101 127 61 71 89 97 79 83 103 109 113 73 10 59 348 Primes 53 to 127
19 53 67 101 127 83 59 79 89 71 109 73 113 61 103 97 107 348
20 53 73 113 109 71 89 79 59 83 127 61 107 67 97 103 101 348
21 53 79 103 113 61 67 107 71 73 97 89 109 101 83 12 59 348
22 53 109 89 97 73 71 107 67 61 113 103 79 59 127 83 101 348
23 67 101 71 109 53 83 103 59 73 113 107 61 97 127 79 89 348

rule-n.gif (1968 bytes)

Order-8B using consecutive primes

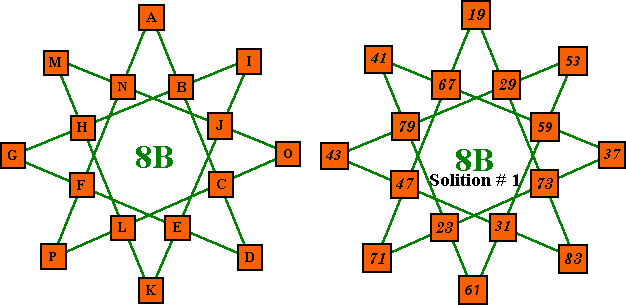
p8b_con-1.gif (8557 bytes)

Consecutive primes solutions, pattern 8B

# A b c D e f G h I j K l M n O P Sum Remarks -8B
1 19 29 73 83 31 47 43 79 53 59 61 23 41 67 37 71 204 Primes 19 to 83
2 19 29 83 73 23 71 37 59 79 41 61 31 53 67 43 47 204
3 19 59 43 83 37 53 31 73 41 47 79 23 29 61 67 71 204
4 19 59 53 73 61 23 47 67 31 41 71 29 37 83 43 79 204
5 19 59 53 73 71 23 37 67 41 31 61 29 47 83 43 79 204
6 19 59 79 47 23 61 73 41 31 67 83 43 37 71 29 53 204
7 19 67 47 71 73 23 37 59 41 29 61 31 53 79 43 83 204
8 19 67 71 47 31 83 43 41 53 59 61 73 29 79 37 23 204
9 23 53 61 67 59 37 41 31 79 19 47 43 83 73 29 71 204
10 23 61 83 37 59 79 29 41 73 19 53 43 67 71 47 31 204
11 29 43 79 53 31 61 59 19 83 23 67 47 71 73 37 41 204
12 29 61 47 67 83 23 31 53 59 19 43 37 71 73 41 79 204
13 29 67 83 61 31 59 89 43 41 71 97 47 53 79 37 73 240 Primes 29 to 97
14 31 41 97 71 37 89 43 73 83 61 59 29 79 53 47 67 240
15 31 41 97 89 59 73 37 101 79 67 53 43 61 83 47 71 258 Primes 31 to 101
16 31 83 101 43 71 97 47 67 61 73 53 79 59 89 37 41 258
17 37 59 73 89 61 41 67 79 53 43 101 31 47 97 71 83 258
18 41 31 89 97 37 71 53 73 101 61 59 43 83 67 47 79 258
19 41 31 97 89 37 79 53 73 101 61 59 43 83 67 47 71 258
20 41 67 61 89 43 73 53 37 101 31 83 79 59 97 71 47 258
21 41 79 37 101 73 31 53 67 59 43 83 61 47 97 71 89 258
22 53 97 71 127 59 73 89 83 79 107 103 101 61 113 67 109 348 Primes 53 to 127
23 53 97 127 71 67 109 101 89 61 113 107 79 73 103 59 83 348
24 53 97 127 71 107 109 61 89 101 73 67 79 113 103 59 83 348
25 59 97 103 89 109 79 71 67 113 53 73 101 107 127 61 83 348
26 59 97 103 89 109 79 71 107 73 53 113 61 67 127 101 83 348
27 61 83 97 107 79 59 103 73 89 67 113 53 109 101 71 127 348
28 61 89 127 71 107 73 97 83 79 59 103 53 109 113 67 101 348
29 61 101 83 103 53 113 79 59 109 97 89 127 73 107 71 67 348

Top.gif (1256 bytes)rule-w.gif (2718 bytes)

Please send me Feedback about my Web site!Aro_up.gif (318 bytes)home07.gif (2303 bytes)

Harvey Heinz   harveyheinz@shaw.ca
Last updated March 01, 2005
Copyright ©  2001 by Harvey D. Heinz