


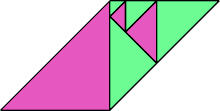
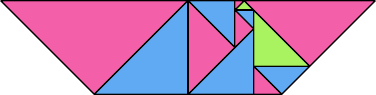
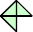
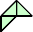
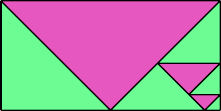
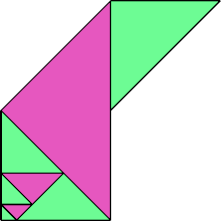
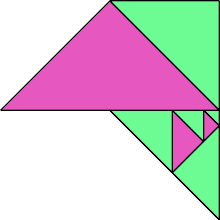
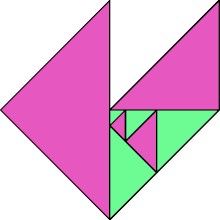
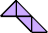
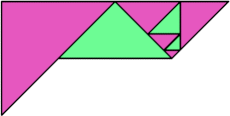
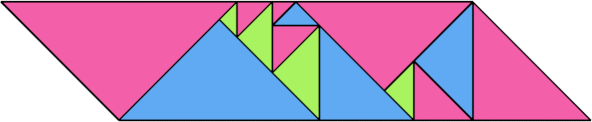
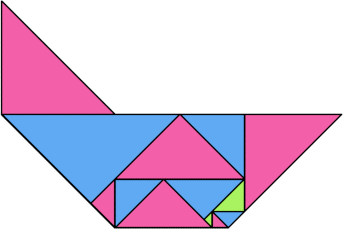
Here I show some minimal known dissections for polytans with up to five cells, omitting polytans that can be obtained by enlarging smaller polytans.
Bryce Herdt pointed out that one of my pentatan tilings could be done with fewer tiles. He also found a tiling of the wrong polytan.

|  |
| 7 | |

|  |
| 7 |

|  |
| 13 | |

|  |
| 2 | |
|  |
| 2 | |
|  |
| 2 |

|  |
| 8 | |

|  |
| 8 | |

|  |
| 8 | |

|  |
| 8 | |

|  |
| 8 | |

|  |
| 8 | |

| 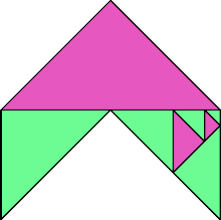 |
| 8 | |

| 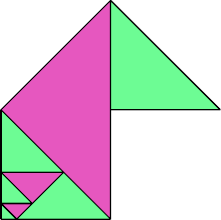 |
| 8 | |
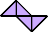
| 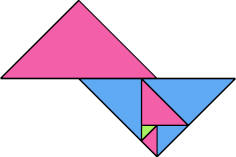 |
| 7 | |
|  |
| 8 | |

|  |
| 15 |

|  |
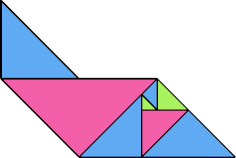
| 13 | |

|  |
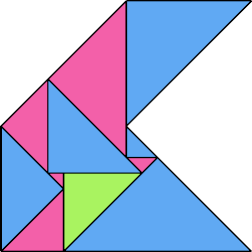
| 8 | |

|  |
| 11 | |

|  |
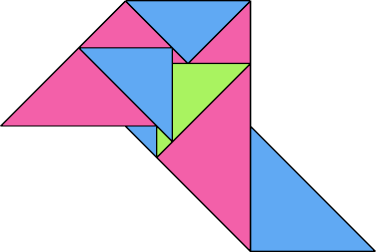
| 13 | |

|  |
| 11 | |

|  |
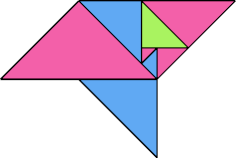
| 11 | |

|  |
| 8 | |

|  |
| 2 | |

|  |
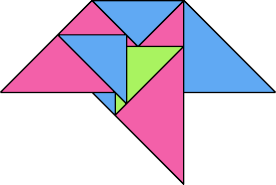
| 8 | |

|  |
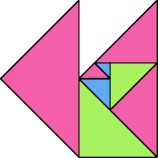
| 11 | |

|  |
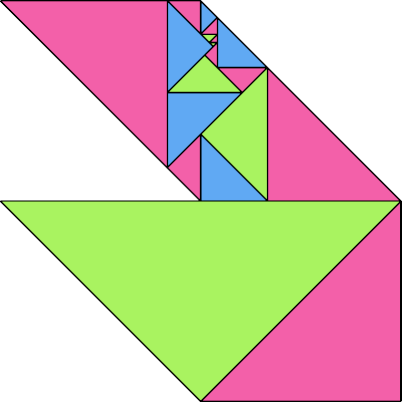
| 8 | |

|  |
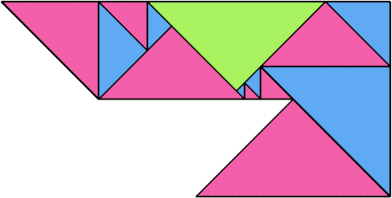
| 14 | |

|  |
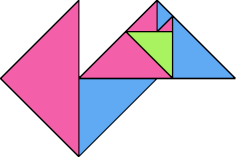
| 14 | |

|  |
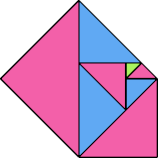
| 8 | |

|  |
| 8 | |

| 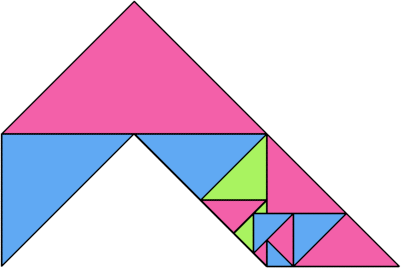 |
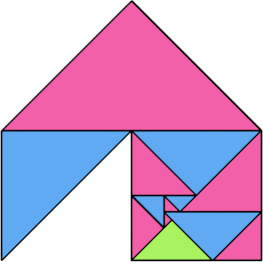
| 14 | |

|  |
| 13 | |
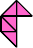
| 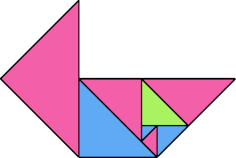 |
| 8 | |

| 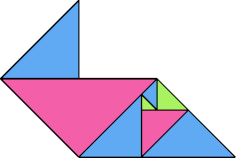 |
| 8 | |

| 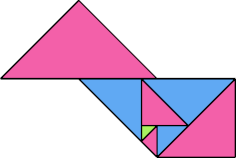 |
| 8 | |

| 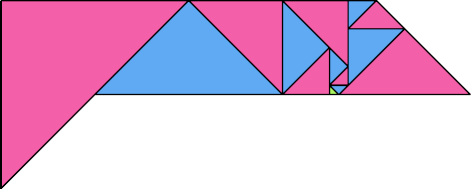 |
| 14 | |

| 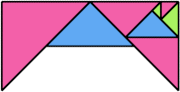 |
| 8 | |

| 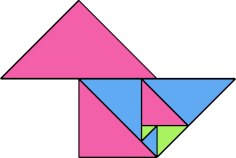 |
| 8 | |

|  |
| 2 | |
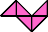
| 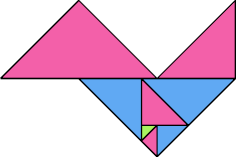 |
| 8 | |

|  |
| 2 | |

| 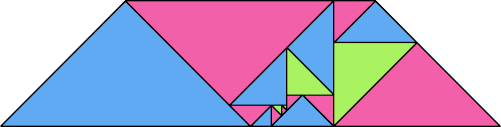 |
| 21 | |

|  |
| 14 | |

|  |
| 2 | |

|  |
| 2 |
Last revised 2025-10-05.