Galvagni Figures for Polyaboloes
A polyabolo is a plane figure formed by
joining equal isosceles right triangles along equal edges.
A Galvagni figure is a figure that can be tiled by a polyform
in more than one way—a kind of self-compatibility figure.
Galvagni figures
first appeared in Erich Friedman's
Math Magic
for November 2004.
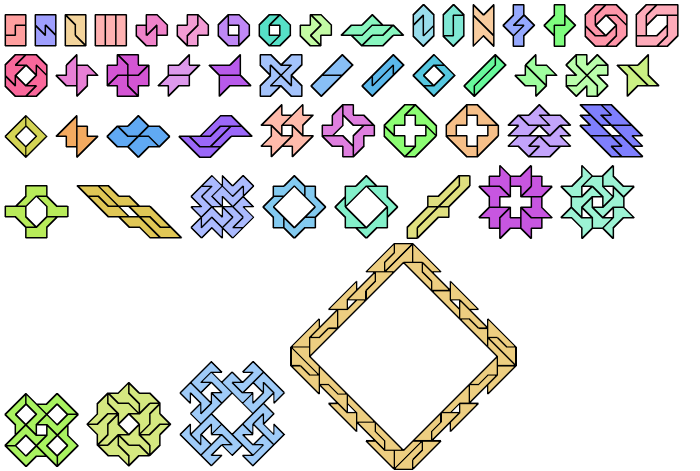
Here are minimal known Galvagni figures for polyaboloes.
Some polyaboloes have solutions that are technically Galvagni
figures but are not polyaboloes.
They are formed by joining parallelograms to make voided rhombuses.


Impossible

Non-polyabolo Solution


Mirror-Symmetry Variant

Holeless

Impossible

Non-polyabolo Solution


Holeless Variant

Impossible

Non-polyabolo Solutions


Holeless Variants
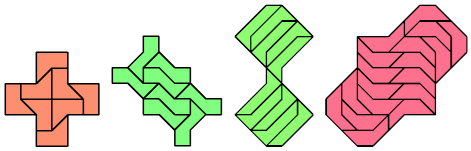
Mirror-Symmetric Variants
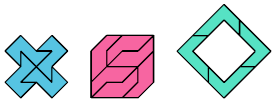
Impossible

Non-polyabolo Solution
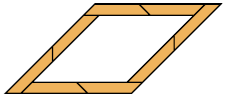
Mirror-Symmetric Variants
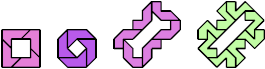
Unsolved or Impossible

Non-polyabolo Solutions

Last revised 2014-10-28.
Back to Galvagni Compatibility
<
Polyform Compatibility
<
Polyform Curiosities
Col. George Sicherman
[ HOME
| MAIL
]





















