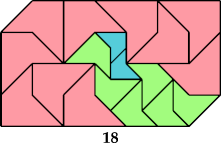
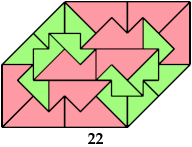
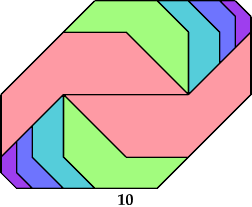
Similar Polyaboloes Forming a Convex Shape

A polyabolo, or polytan, is a plane figure formed by joining equal isosceles right triangles along equal edges.

How few similar (scaled) copies of a given polyabolo can form a convex shape? For most polyaboloes, the tilings with the fewest tiles use equal tiles, as with this triabolo:

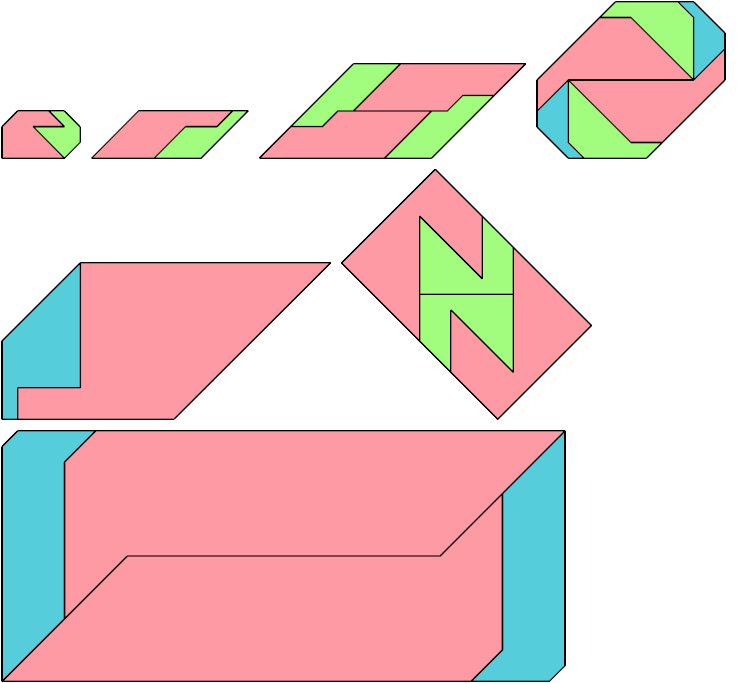
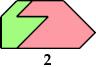
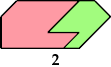
Here I show the only polyaboloes I know of for which the convex tiling with the fewest tiles uses tiles of different sizes. If you find another such polyabolo, or a tiling with fewer tiles than shown, please write.

So far as I know, these three polyaboloes cannot tile any convex shape at a uniform scale.

See also Similar Polyaboloes Tiling a Triangle, Similar Polyaboloes Tiling a Square, Similar Polyaboloes Tiling an Octagon, and Similar Polyiamonds Forming a Convex Shape.

Last revised 2024-04-26.

Back to Polyform Tiling < Polyform Curiosities
Col. George Sicherman [ HOME | MAIL ]