Polydrafter Bireptiles

Introduction

In combinatorial geometry a reptile is a geometric figure, equal copies of which can be joined to form an enlarged form of the figure. For example, four copies of the P-tridrafter can form a P-tridrafter at double scale, or four times as large:

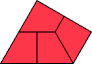
Reptiles are known for polyominoes, polyiamonds, polyaboloes, polydrafters, and other polyforms.

Few polyforms of any kind form reptiles. A bireptile is a figure of which copies can be joined to form two joined, equally enlarged copies of the original figure.

Any figure with a reptiling trivially has a bireptiling, but not every figure with a bireptiling has a reptiling. That is, bireptiles are more common than reptiles.

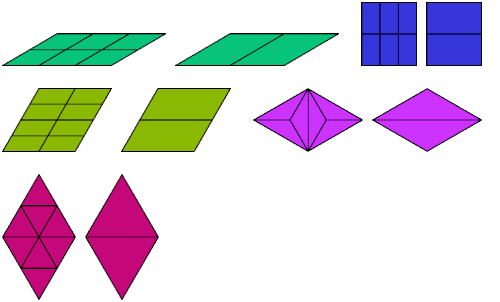
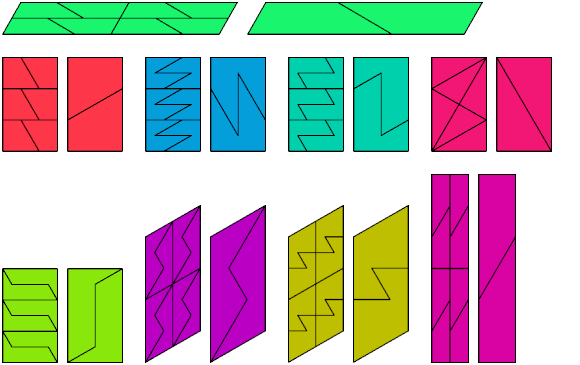
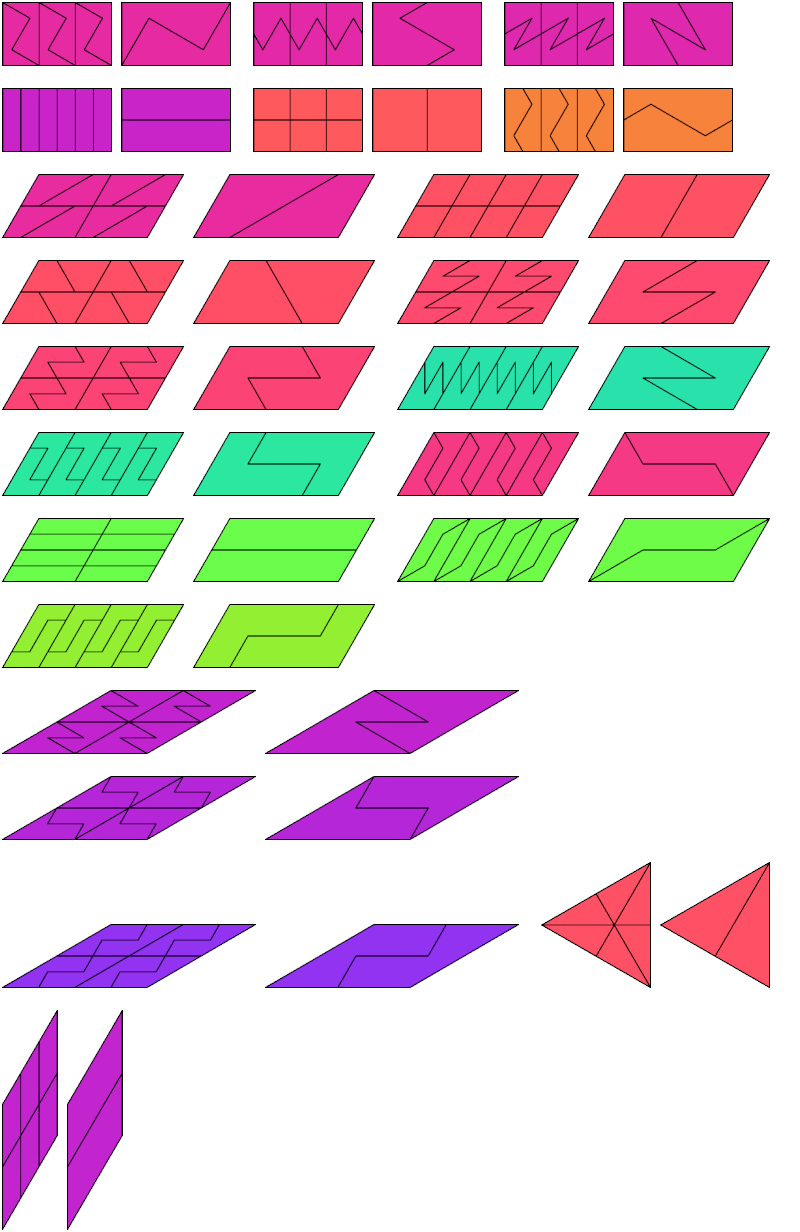
Below I show minimal known bireptilings for various polydrafters.

Number of
Cells Number of
Reptiles Number of
Bireptiles

1 1 1

2 5 5

3 2 9

4 9 22

Number of Cells	Number of Reptiles	Number of Bireptiles
1	1	1
2	5	5
3	2	9
4	9	22

Didrafters

Tridrafters

Tetradrafters

Last revised 2015-12-11.

Back to Polydrafter Tiling < Polyform Tiling < Polyform Curiosities

Col. George Sicherman { HOME | MAIL }