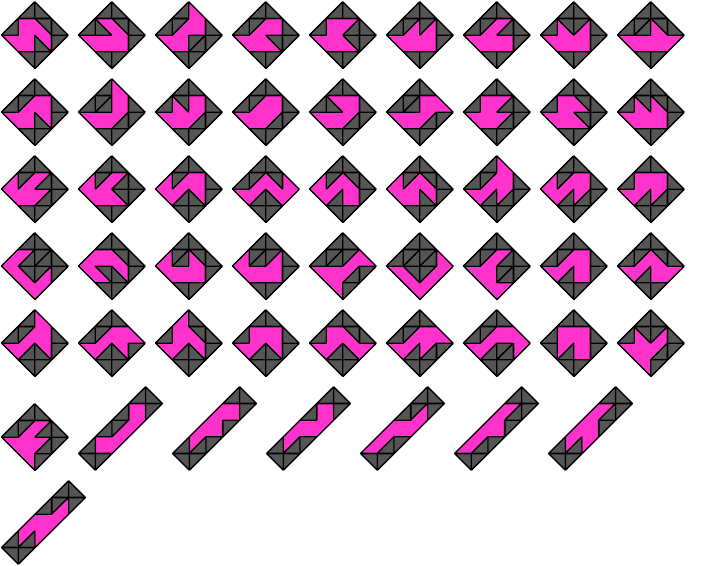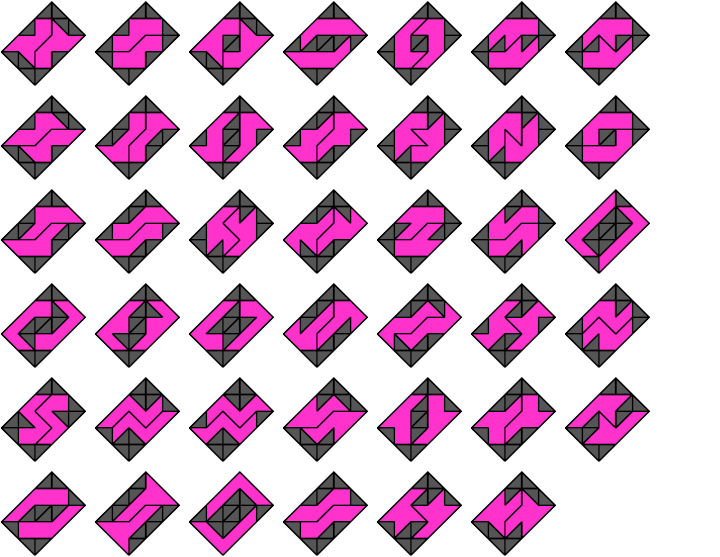Oblique Rectification Numbers for Polyaboloes
Introduction
A polyabolo or polytan is a plane figure formed
by joining equal isosceles right triangles edge to equal edge.
In issue 14
of Rodolfo M. Kurchan's
Puzzle Fun,
Gustavo Piñeiro defines the rectification number
of a polyomino as the least number of cells that can be left vacant
when copies of the polyomino are packed in a rectangle.
Here I investigate the same problem for polyaboloes, using
oblique rectangles instead of orthogonal rectangles.
In the results below, I omit polyaboloes that can be
obliquely rectified—that is, that can tile some
oblique rectangle.
Such polyaboloes have Rectification Number 0.
Thanks to Joyce Michel for suggesting this variant.
See also Rectification Numbers
for Polyaboloes.
Diaboloes
4 Vacant Cells
6 Vacant Cells
Triaboloes
1 Vacant Cell

2 Vacant Cells

4 Vacant Cells

Tetraboloes
4 Vacant Cells
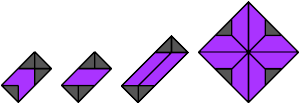
8 Vacant Cells
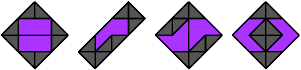
12 Vacant Cells

Pentaboloes
2 Vacant Cells

3 Vacant Cells

4 Vacant Cells

6 Vacant Cells
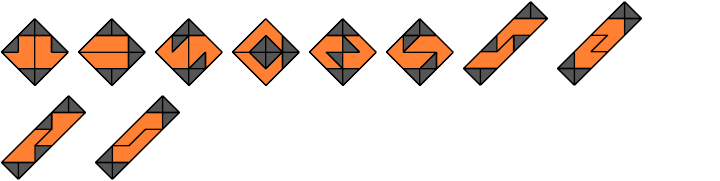
7 Vacant Cells

11 Vacant Cells
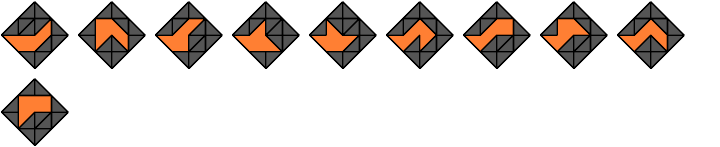
Hexaboloes
2 Vacant Cells

4 Vacant Cells
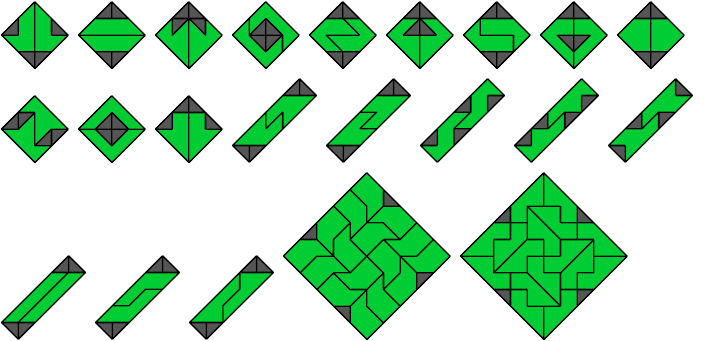
6 Vacant Cells
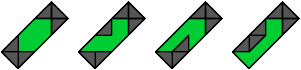
8 Vacant Cells
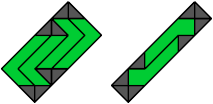
10 Vacant Cells

12 Vacant Cells

18 Vacant Cells
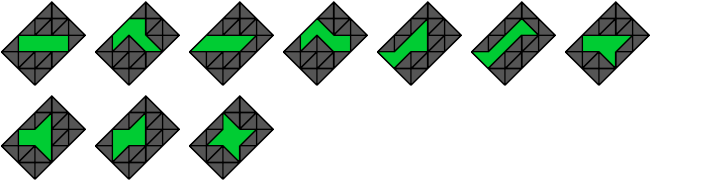
Heptaboloes
1 Vacant Cell

2 Vacant Cells
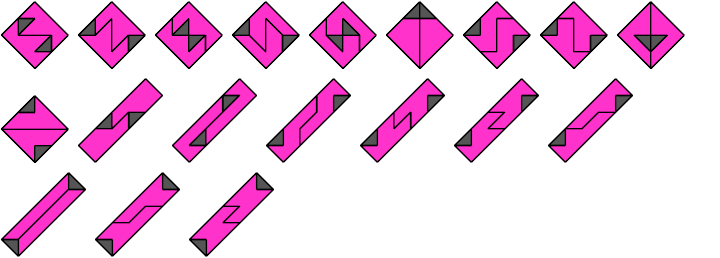
4 Vacant Cells

5 Vacant Cells
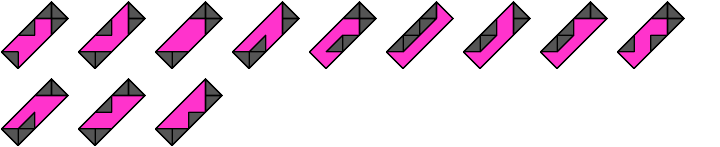
6 Vacant Cells
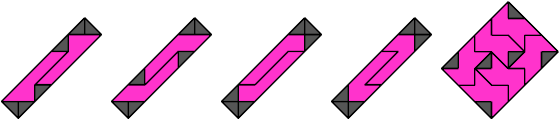
8 Vacant Cells

9 Vacant Cells
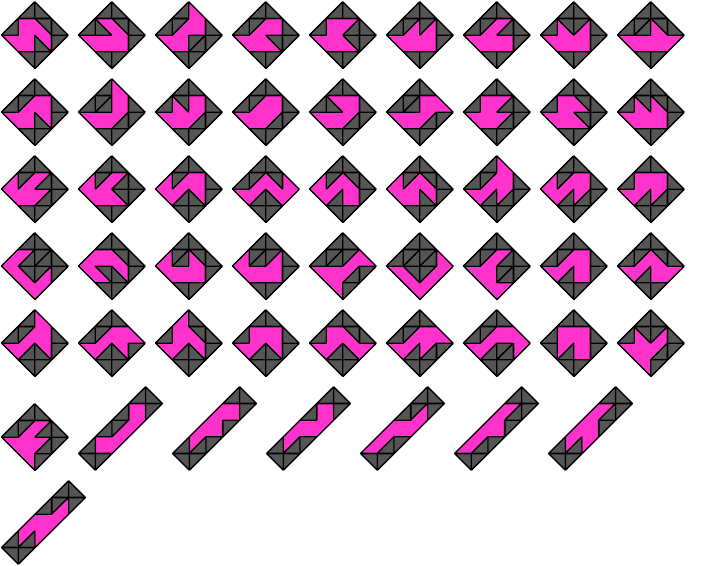
10 Vacant Cells
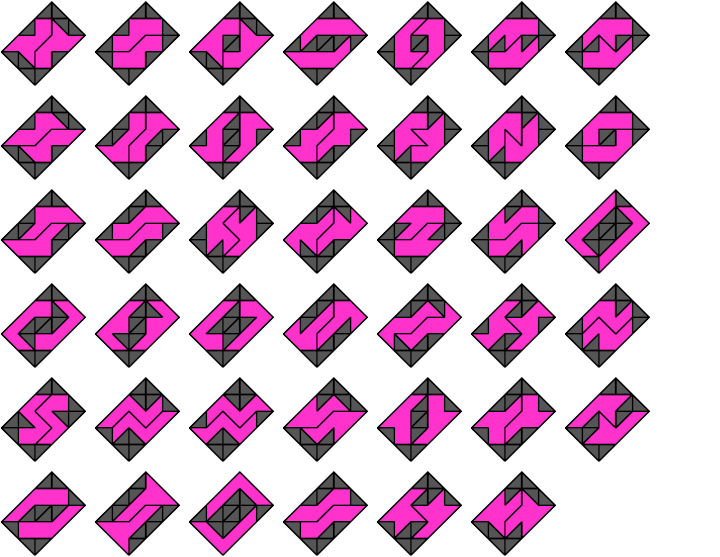
12 Vacant Cells

15 Vacant Cells
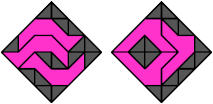
17 Vacant Cells

Last revised 2023-09-09.
Back to Polyabolo Tiling
< Polyform Tiling
< Polyform Curiosities
Col. George Sicherman
[ HOME
| MAIL
]