Rectification Numbers for Polyaboloes
Introduction
A polyabolo or polytan is a plane figure formed
by joining equal isosceles right triangles edge to equal edge.
In issue 14
of Rodolfo M. Kurchan's
Puzzle Fun,
Gustavo Piñeiro defines the rectification number
of a polyomino as the least number of cells that can be left vacant
when copies of the polyomino are packed in a rectangle.
Here I investigate the same problem for polyaboloes.
In the results below, I omit polyaboloes that can be
rectified—that is, that can tile some rectangle.
Such polyaboloes have Rectification Number 0.
See also Oblique Rectification
Numbers for Polyaboloes.
Triaboloes
2 Vacant Cells

5 Vacant Cells

Tetraboloes
2 Vacant Cells
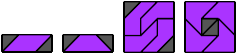
4 Vacant Cells

8 Vacant Cells

Pentaboloes
2 Vacant Cells

3 Vacant Cells

4 Vacant Cells
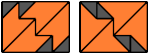
6 Vacant Cells

7 Vacant Cells

8 Vacant Cells

12 Vacant Cells

13 Vacant Cells

Hexaboloes
2 Vacant Cells

4 Vacant Cells

6 Vacant Cells
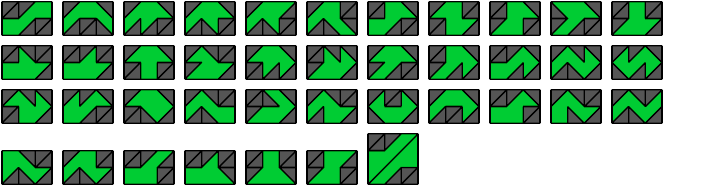
8 Vacant Cells
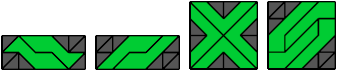
10 Vacant Cells

12 Vacant Cells

18 Vacant Cells

Heptaboloes
1 Vacant Cell

2 Vacant Cells

4 Vacant Cells

5 Vacant Cells

6 Vacant Cells

9 Vacant Cells

10 Vacant Cells

11 Vacant Cells

16 Vacant Cells

17 Vacant Cells

18 Vacant Cells

22 Vacant Cells

25 Vacant Cells

Last revised 2023-09-07.
Back to Polyabolo Tiling
< Polyform Tiling
< Polyform Curiosities
Col. George Sicherman
[ HOME
| MAIL
]
































