Convex Polygons From Pairs of Polytans

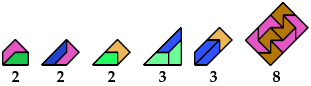
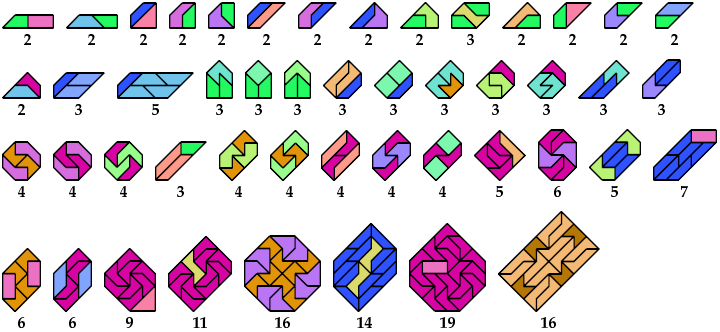
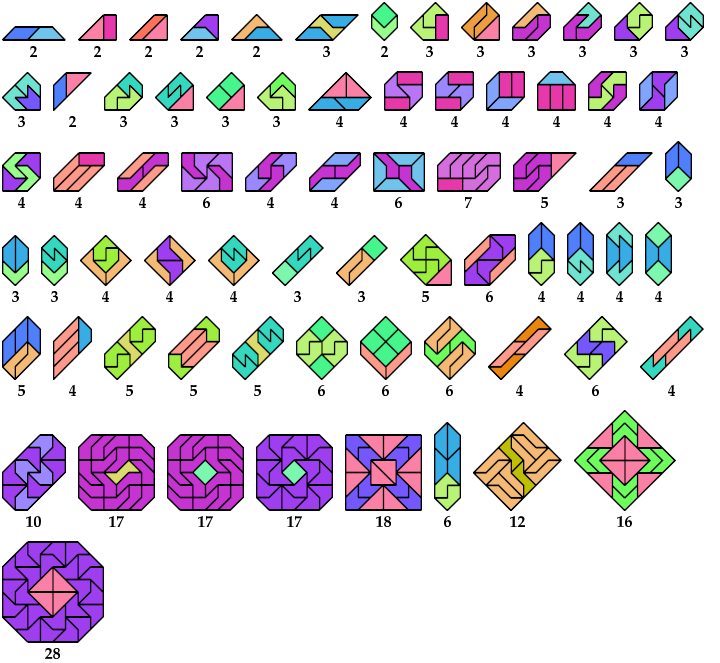
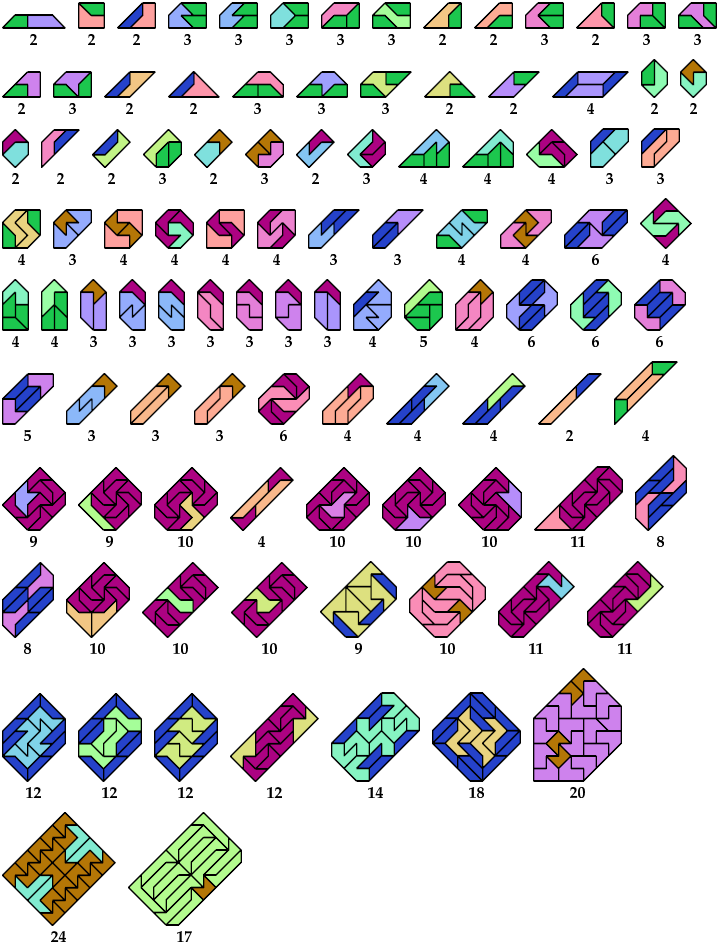
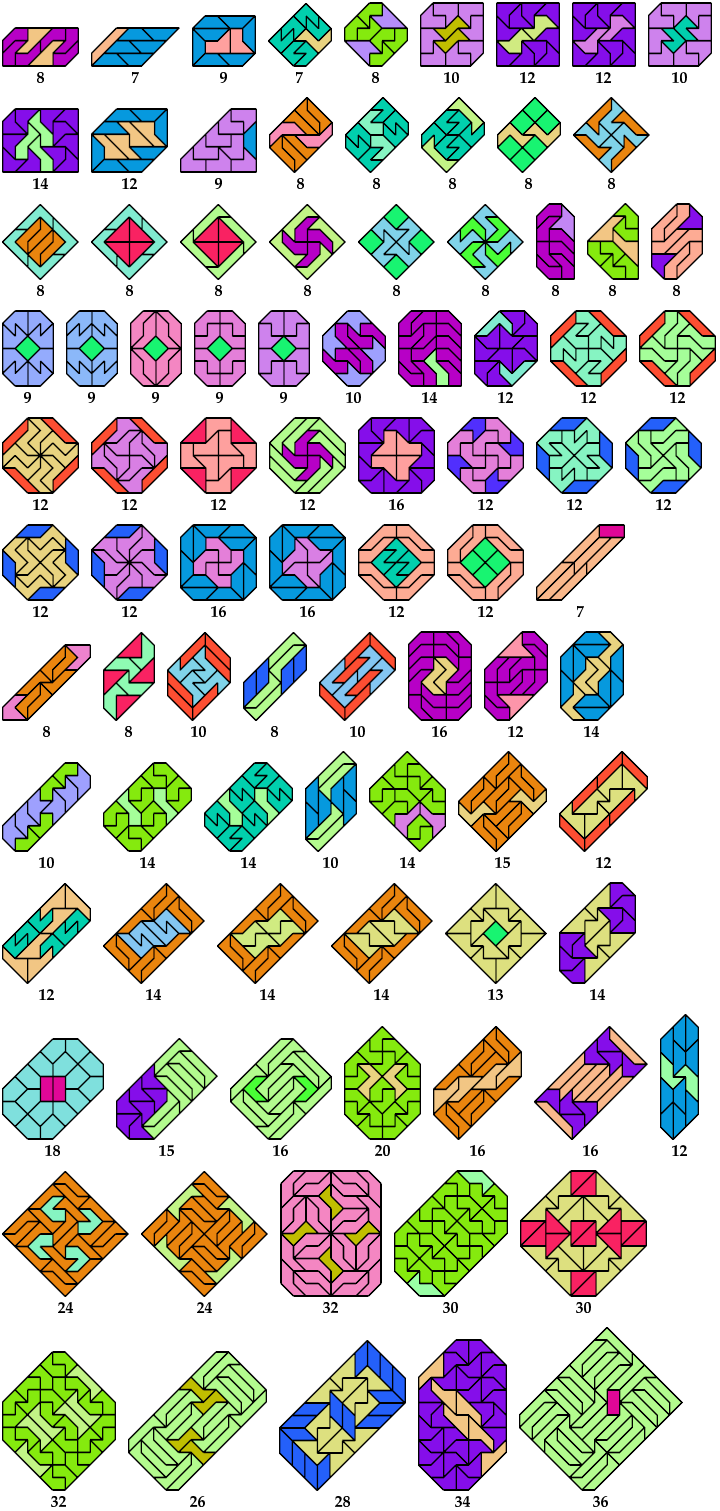
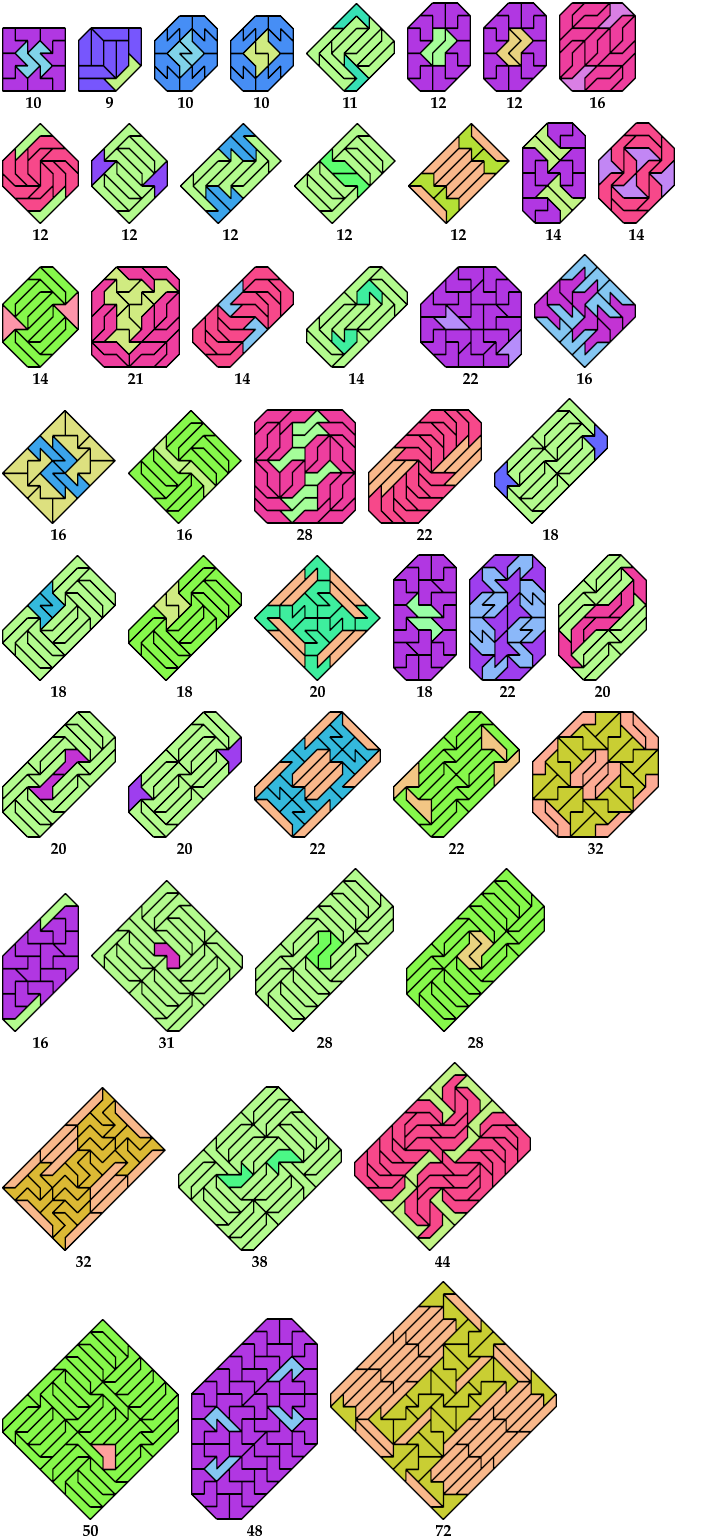
Here I show minimal known convex polygons formed by pairs of polytans with 3 through 5 cells. If you find a smaller solution or solve an unsolved case, please write.

At Math Magic for April 1999, Erich Friedman considers for various plane shapes the set of values of n for which n copies of the shape can form a convex shape. Ed Pegg Jr. also considers this problem at Dissections of Convex Figures.

Tritans and Tritans

	•	3	3	2
	3	•	2	2
	3	2	•	8
	2	2	8	•

Tritans and Tetratans

	7	2	6	19
	2	2	4	4
	2	2	16	6
	3	2	?	4
	3	2	?	6
	5	2	?	2
	3	3	3	3
	3	3	?	4
	?	3	4	4
	5	2	4	3
	14	3	?	11
	3	2	16	5
	2	3	?	4
	2	2	?	9

Tetratans and Tetratans

	•	7	4	4	4	4	?	?	?	3	?	?	4	2
	7	•	6	4	4	6	3	17	?	4	17	3	4	5
	4	6	•	10	4	2	3	17	4	3	?	4	6	28
	4	4	10	•	?	?	3	?	?	6	?	?	?	18
	4	4	4	?	•	2	4	3	?	4	?	5	3	2
	4	6	2	?	2	•	4	4	3	6	3	2	4	4
	?	3	3	3	4	4	•	3	3	3	5	4	4	3
	?	17	17	?	3	4	3	•	2	6	?	3	6	3
	?	?	4	?	?	3	3	2	•	3	?	6	?	16
	3	4	3	6	4	6	3	6	3	•	5	4	5	5
	?	17	?	?	?	3	5	?	?	5	•	12	?	?
	?	3	4	?	5	2	4	3	6	4	12	•	4	3
	4	4	6	?	3	4	4	6	?	5	?	4	•	2
	2	5	28	18	2	4	3	3	16	5	?	3	2	•

Tritans and Pentatans

	8	3	10	6
	2	3	4	3
	?	3	4	4
	6	3	3	3
	8	3	?	10
	5	2	20	3
	6	3	?	10
	3	2	?	10
	4	2	3	3
	6	3	?	9
	4	3	3	3
	3	3	3	3
	4	4	?	2
	12	4	?	11
	3	3	2	2
	?	4	24	3
	14	4	2	4
	6	2	?	4
	?	4	?	4
	12	3	?	10
	4	5	17	9
	2	3	?	11
	12	3	?	10
	9	2	?	12
	18	4	?	10
	2	2	?	10
	2	4	3	4
	3	2	3	4
	2	2	4	4
	2	2	?	11

Tetratans and Pentatans

	6	5	6	?	2	4	4	?	6	?	?	8	6	6
	6	3	3	4	4	4	6	9	?	5	32	5	3	3
	?	?	4	?	?	3	3	2	?	3	?	8	?	?
	3	3	3	12	6	16	?	9	?	2	?	6	5	3
	?	5	12	?	12	16	?	?	?	14	?	6	12	?
	3	3	3	6	6	9	10	9	?	2	10	6	5	3
	?	8	?	?	?	6	6	?	?	6	?	?	?	?
	?	4	?	?	?	?	6	?	?	8	?	?	4	?
	2	3	3	3	2	2	3	3	3	3	6	5	4	2
	?	10	?	?	?	?	6	?	?	10	?	?	?	?
	6	3	3	3	4	4	2	9	3	3	?	6	5	3
	6	3	3	3	4	4	2	9	?	6	?	6	4	3
	?	2	6	?	?	4	4	?	?	6	?	14	10	?
	?	?	?	?	?	4	4	8	8	5	?	8	10	?
	18	2	2	2	3	4	3	2	2	3	3	3	3	3
	?	?	12	?	?	?	5	3	?	5	3	8	?	8
	?	5	4	2	12	?	8	?	?	2	?	24	12	?
	2	6	6	?	6	?	?	?	6	5	?	?	?	8
	6	2	4	?	?	12	?	?	?	30	?	4	?	6
	?	14	14	?	12	6	14	?	?	14	?	6	12	?
	36	12	15	6	8	10	4	6	16	5	26	6	2	8
	?	8	?	?	?	?	8	?	?	32	?	24	?	?
	?	6	12	?	?	4	6	?	?	4	?	14	?	?
	3	5	14	?	28	4	6	13	?	4	?	14	12	30
	?	16	?	?	12	14	7	8	?	20	?	15	12	?
	?	8	34	4	4	12	12	?	?	8	?	16	?	?
	7	4	16	3	4	7	3	4	?	5	?	6	2	2
	?	3	8	3	4	6	12	12	?	6	?	2	4	3
	4	4	16	6	5	9	?	?	5	4	?	6	?	12
	?	12	?	?	?	2	3	6	?	3	?	6	?	?

6 Tiles or Less

7 Tiles or More

Pentatans and Pentatans

	•	3	8	3	?	3	14	4	2	?	3	3	14	?	5	?	4	?	?	?	12	44	?	?	?	4	22	6	6	?
	3	•	?	6	16	5	8	4	6	6	6	6	2	4	3	?	?	3	?	28	20	6	21	8	?	3	3	5	3	3
	8	?	•	?	?	?	?	?	3	?	4	?	8	6	2	?	?	4	?	?	6	4	?	?	?	?	?	?	6	?
	3	6	?	•	?	2	?	3	3	6	?	8	?	?	4	?	?	3	?	?	31	?	?	3	?	3	6	6	3	3
	?	16	?	?	•	6	?	?	6	?	?	6	16	?	4	4	?	?	4	?	20	?	?	?	?	?	4	3	?	?
	3	5	?	2	6	•	6	22	3	4	6	4	48	10	3	?	2	3	18	12	16	14	8	4	12	3	5	6	3	3
	14	8	?	?	?	6	•	?	7	?	8	22	4	?	4	4	?	?	?	?	20	?	?	?	?	?	?	?	?	?
	4	4	?	3	?	22	?	•	3	?	5	3	?	?	2	?	2	?	?	?	12	?	?	?	?	?	3	3	?	?
	2	6	3	3	6	3	7	3	•	4	3	3	5	6	3	5	4	2	4	6	7	9	7	3	6	3	7	4	3	3
	?	6	?	6	?	4	?	?	4	•	6	4	?	?	5	?	4	?	?	?	18	?	?	?	?	?	6	4	?	?
	3	6	4	?	?	6	8	5	3	6	•	2	4	8	4	4	?	3	4	?	4	4	?	5	?	3	8	6	3	3
	3	6	?	8	6	4	22	3	3	4	2	•	4	10	?	?	4	3	?	?	3	8	10	8	?	3	3	6	3	3
	14	2	8	?	16	48	4	?	5	?	4	4	•	?	4	8	?	?	?	?	12	?	?	16	?	2	4	?	?	?
	?	4	6	?	?	10	?	?	6	?	8	10	?	•	4	8	?	?	?	?	18	?	?	?	?	?	22	?	?	?
	5	3	2	4	4	3	4	2	3	5	4	?	4	4	•	4	4	?	3	4	3	4	4	4	3	2	4	3	2	2
	?	?	?	?	4	?	4	?	5	?	4	?	8	8	4	•	4	?	?	4	11	?	8	8	4	?	?	?	4	8
	4	?	?	?	?	2	?	2	4	4	?	4	?	?	4	4	•	6	4	?	14	?	4	2	?	?	20	?	8	?
	?	3	4	3	?	3	?	?	2	?	3	3	?	?	?	?	6	•	?	?	38	?	?	4	?	4	6	?	4	?
	?	?	?	?	4	18	?	?	4	?	4	?	?	?	3	?	4	?	•	4	12	?	?	?	4	?	?	2	2	6
	?	28	?	?	?	12	?	?	6	?	?	?	?	?	4	4	?	?	4	•	28	?	?	?	?	?	?	6	?	?
	12	20	6	31	20	16	20	12	7	18	4	3	12	18	3	11	14	38	12	28	•	16	18	8	28	22	2	3	50	14
	44	6	4	?	?	14	?	?	9	?	4	8	?	?	4	?	?	?	?	?	16	•	?	?	?	?	?	?	?	?
	?	21	?	?	?	8	?	?	7	?	?	10	?	?	4	8	4	?	?	?	18	?	•	?	?	?	12	4	8	?
	?	8	?	3	?	4	?	?	3	?	5	8	16	?	4	8	2	4	?	?	8	?	?	•	?	?	72	32	4	?
	?	?	?	?	?	12	?	?	6	?	?	?	?	?	3	4	?	?	4	?	28	?	?	?	•	?	32	?	?	?
	4	3	?	3	?	3	?	?	3	?	3	3	2	?	2	?	?	4	?	?	22	?	?	?	?	•	4	4	?	?
	22	3	?	6	4	5	?	3	7	6	8	3	4	22	4	?	20	6	?	?	2	?	12	72	32	4	•	6	6	?
	6	5	?	6	3	6	?	3	4	4	6	6	?	?	3	?	?	?	2	6	3	?	4	32	?	4	6	•	8	?
	6	3	6	3	?	3	?	?	3	?	3	3	?	?	2	4	8	4	2	?	50	?	8	4	?	?	6	8	•	?
	?	3	?	3	?	3	?	?	3	?	3	3	?	?	2	8	?	?	6	?	14	?	?	?	?	?	?	?	?	•

8 Tiles or Less

9 Tiles or More

Last revised 2020-06-11.