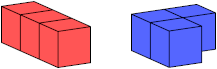

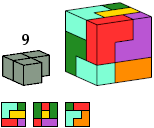
Polycubes can belong to any of 33 symmetry classes, including asymmetry; see Polycube Symmetries. Of these symmetry classes, 31 have even order and can be symmetries of oddities.
Here I show minimal oddities for the L tricube that belong to every even symmetry class. The minimal oddities of the I tricube are not interesting. They include only the tricube itself and the 3×3×3 cube.
If you find a smaller example for any symmetry class, please write.
For pentacubes, see Pentacube Oddities with Full Symmetry and Pentacube Oddities with Inverse Symmetry.
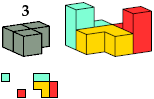
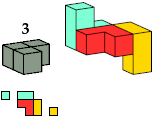
| C4 2 * | B6 2 | K6 2 * | F5 2 * |
|---|---|---|---|
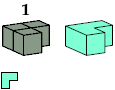
| 
| 
| 
|
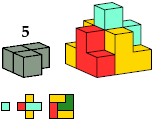
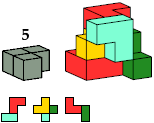
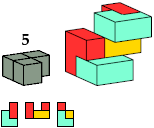
| E4 2 * | A12 4 * | J10 4 * | BC10 4 |

| 
| 
| 
|
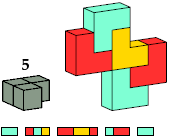
| BB10 4 | CK6 4 * | BE4 4 | CE3 4 * |
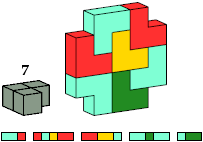
| 
| 
| 
|
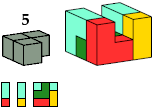
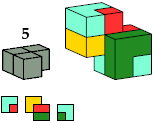
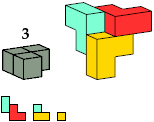
| BF6 4 * | EE4 4 | CD10 6 | FF4 6 * |

| 
| 
| 
|
| H12 6 * | AB16 8 * | EF6 8 * | BFF8 8 |

| 
| 
| 
|
| CJ6 8 * | AE8 8 * | EFF7 8 * | EEE6 8 * |

| 
| 
| 
|
| BD34 12 * | CF6 12 * | BBC2 16 * | R56 24 * |
| 
| 
| 
|
| CCC20 24 * | DEE25 24 * | G1 48 * | |

| 
|  |
Last revised 2025-05-15.