

A pentacube is a solid made of 5 equal cubes joined face to face. There are 29 pentacubes, counting distinct mirror images.
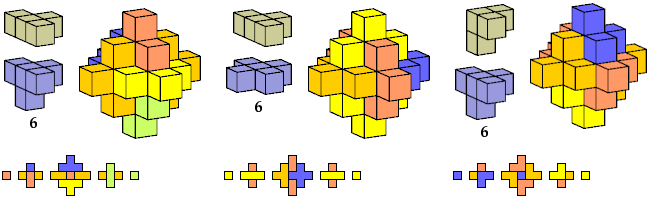
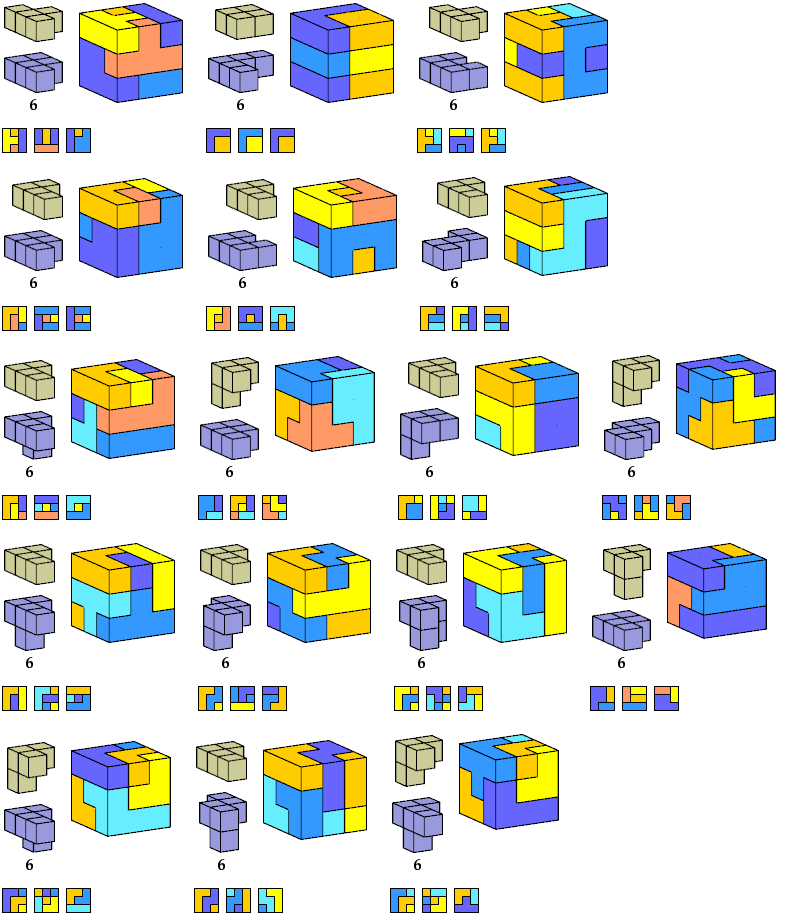
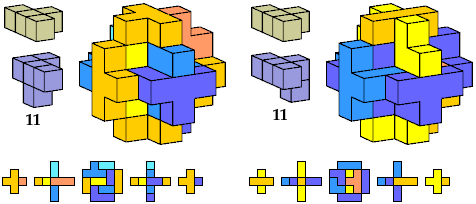
A polyform oddity or Sillke Figure is a polyform with binary symmetry at least, tiled by an odd number of copies of a given polyform.
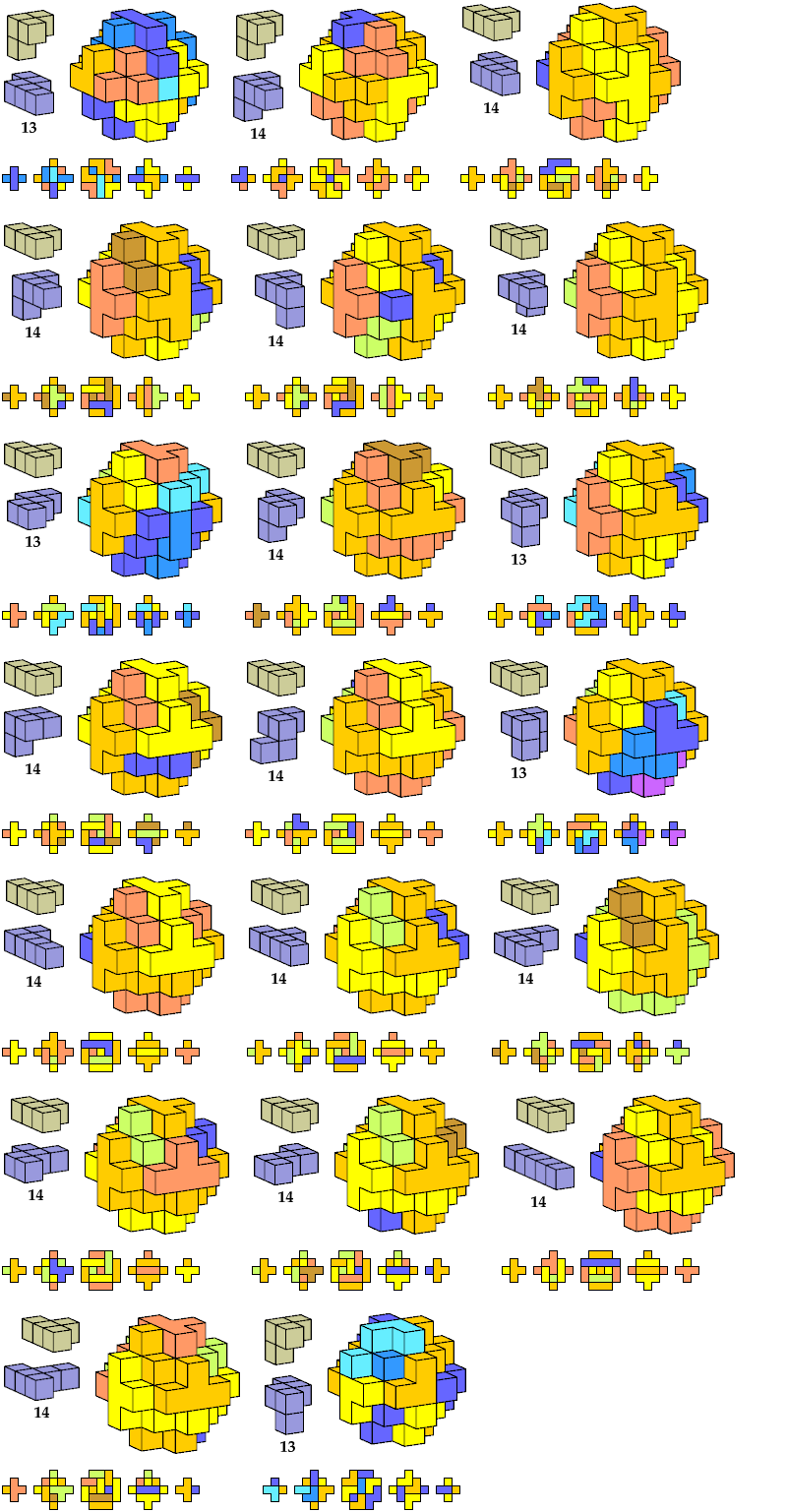
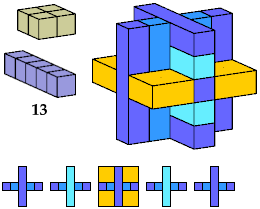
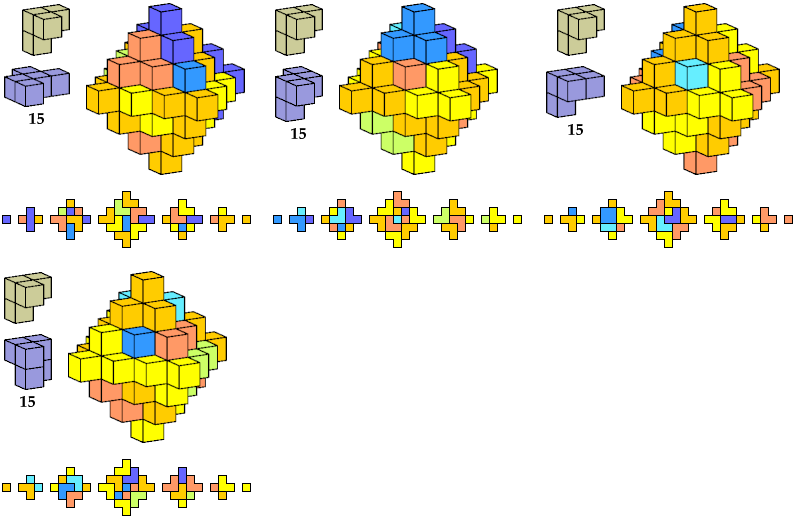
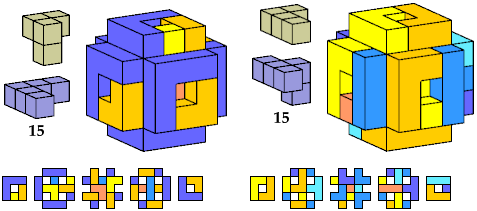
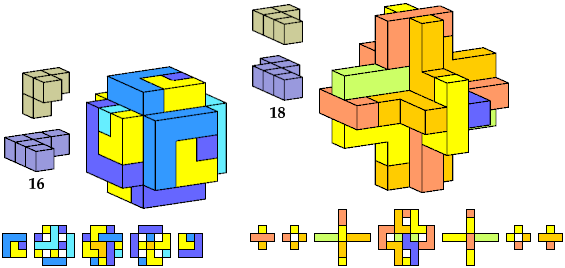
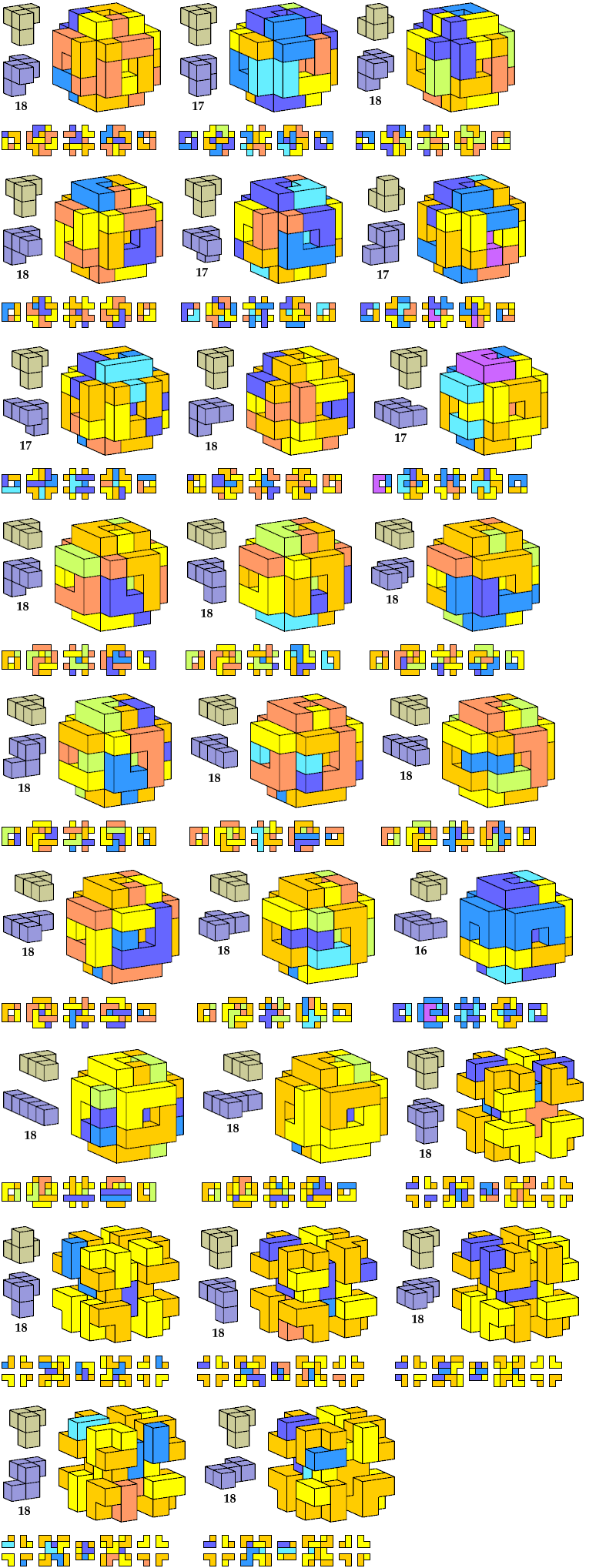
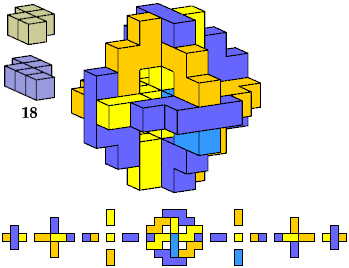
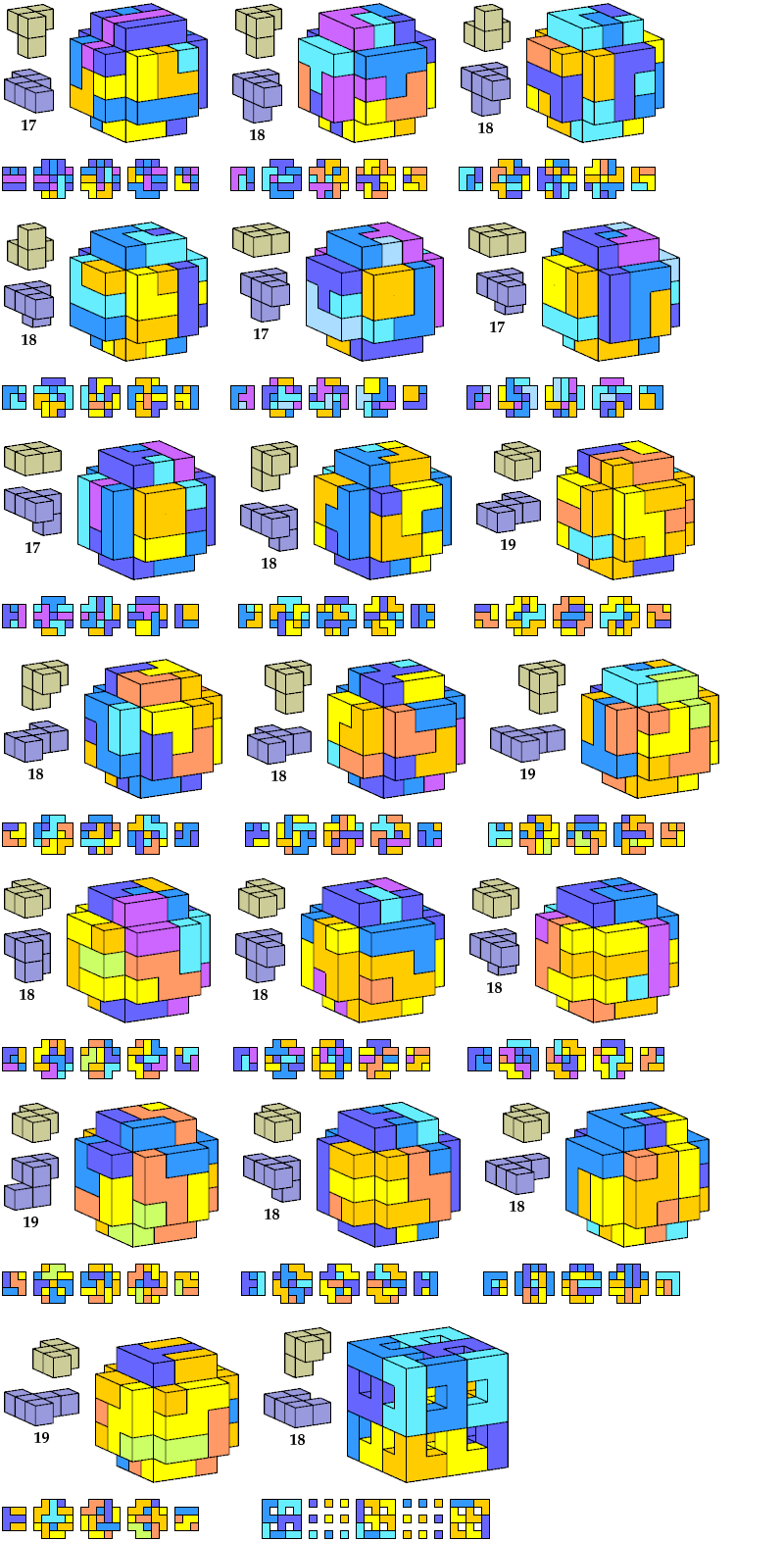
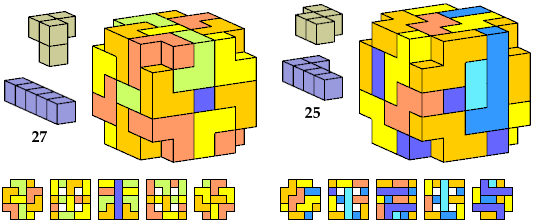
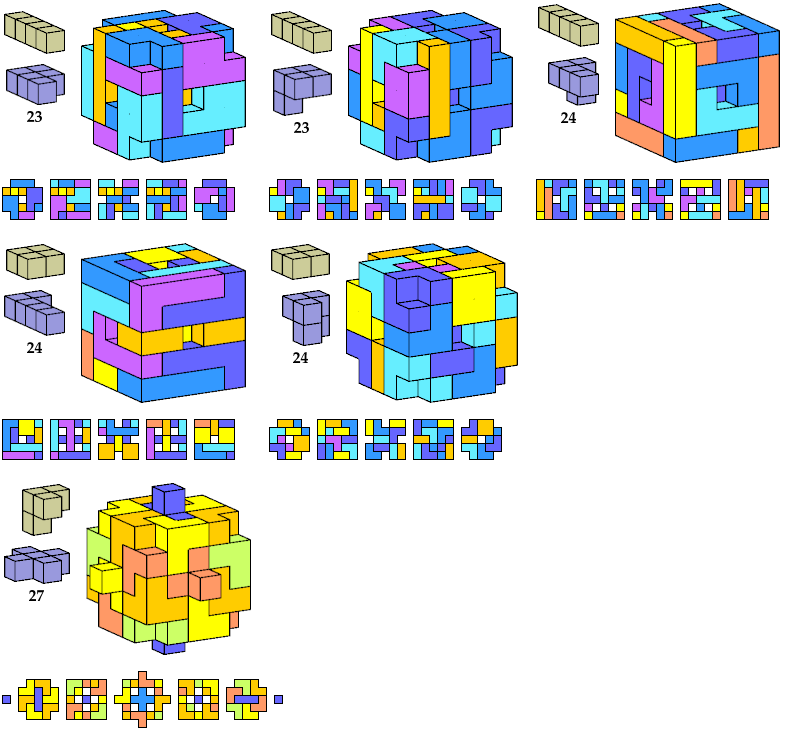
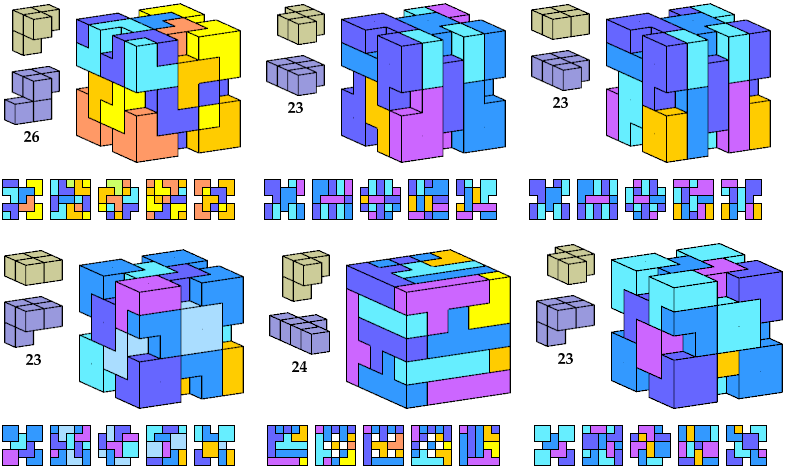
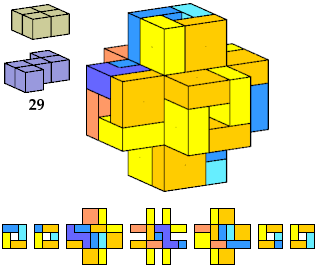
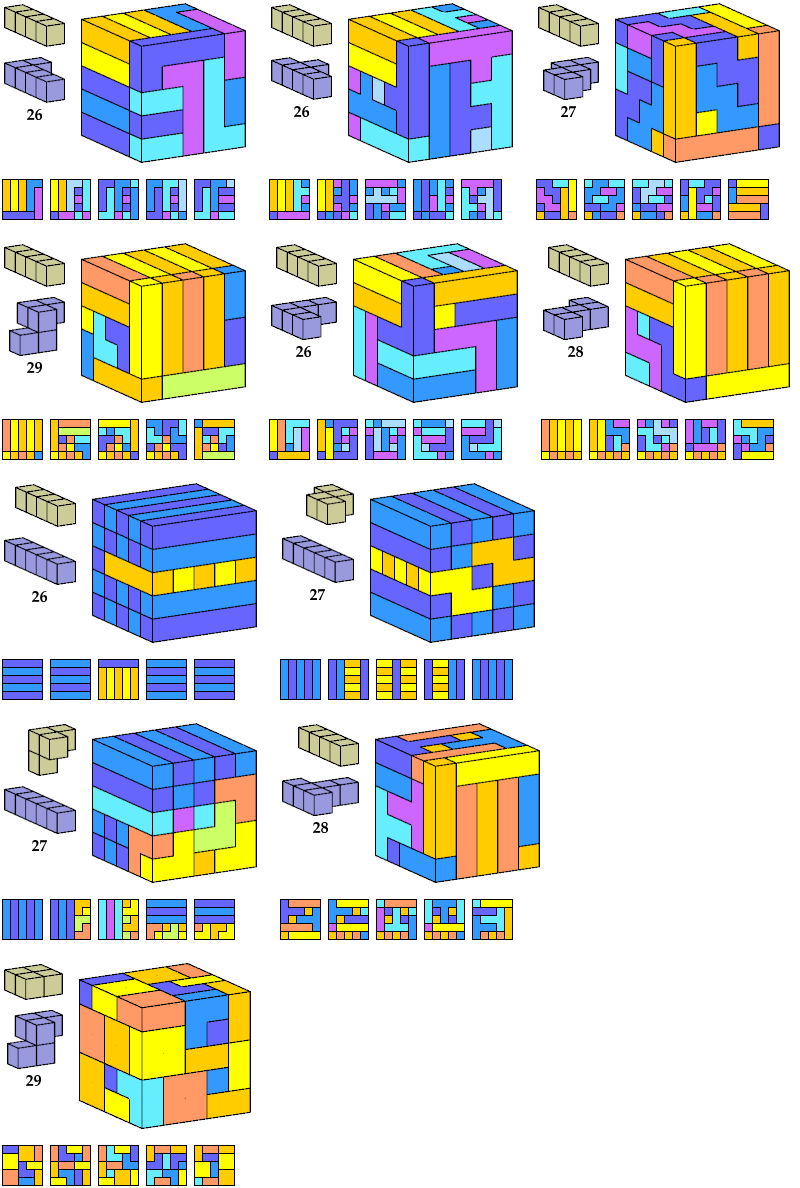
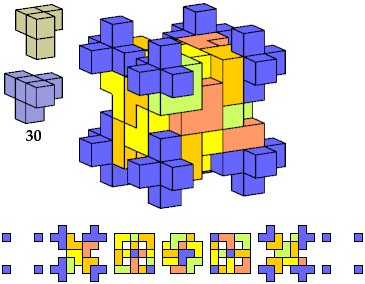
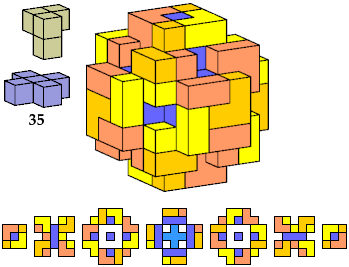
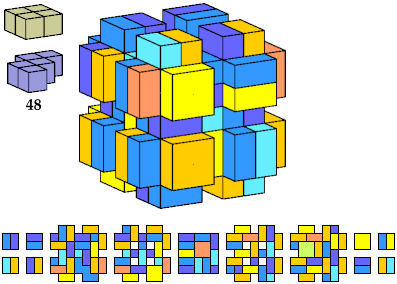
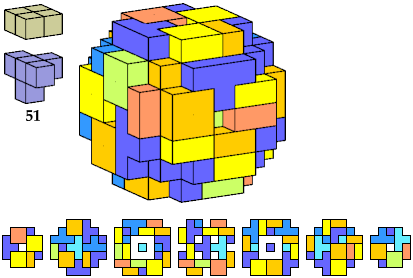
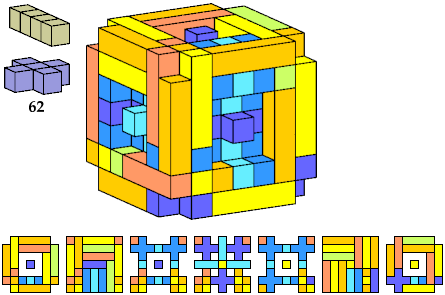
Here I show polycubes with full symmetry and an odd number of cells, formed by joining copies of a given tetracube and a given pentacube. The solutions are the smallest known to me. The figures shown are the numbers of tiles used.
If you find a smaller solution, please write.
See also Pentacube Pair Oddities.
| A | B | E | F | G | H | I | J | K | L | M | N | P | Q | R | S | T | U | V | W | X | Y | Z | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| I | 119 | 119 | 119 | 117 | 125 | 117 | 125 | 111 | 117 | 125 | 87 | 117 | 111 | 111 | 117 | 117 | 125 | 117 | 125 | 125 | 267 | 125 | 125 |
| K | 63 | 81 | 27 | 63 | 113 | 57 | 125 | 27 | 57 | 93 | 25 | 57 | 27 | 63 | 63 | 93 | 93 | 81 | 73 | 27 | 111 | 113 | 81 |
| L | 27 | 67 | 27 | 75 | 75 | 27 | 75 | 27 | 75 | 75 | 93 | 73 | 27 | 27 | 27 | 75 | 75 | 27 | 75 | 75 | 105 | 75 | 27 |
| N | 81 | 81 | 81 | 99 | 81 | 117 | 125 | 81 | 119 | 109 | 117 | 79 | 113 | 113 | 117 | 117 | 81 | 75 | 81 | 117 | 117 | 105 | 81 |
| Q | 111 | 81 | 81 | 117 | 125 | 117 | 61 | 81 | 119 | 111 | 225 | 117 | 113 | 113 | 117 | 117 | 117 | 119 | 27 | 213 | ? | 117 | 123 |
| S | 75 | 75 | 81 | 81 | 75 | 75 | 109 | 75 | 75 | 87 | 129 | 81 | 27 | 75 | 75 | 75 | 81 | 75 | 67 | 75 | 147 | 87 | 75 |
| S′ | 81 | 75 | 75 | 81 | 75 | 87 | |||||||||||||||||
| T | 57 | 49 | 49 | 57 | 57 | 57 | 57 | 57 | 57 | 57 | 25 | 57 | 27 | 57 | 57 | 57 | 57 | 27 | 57 | 57 | 25 | 57 | 57 |
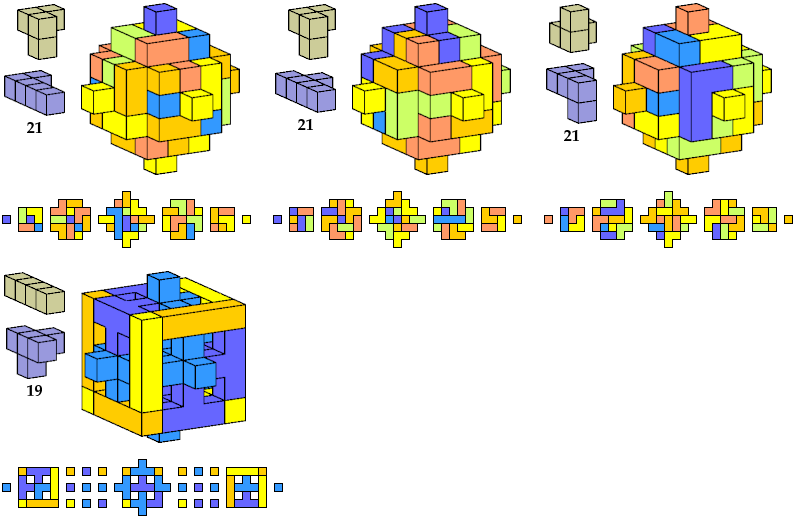
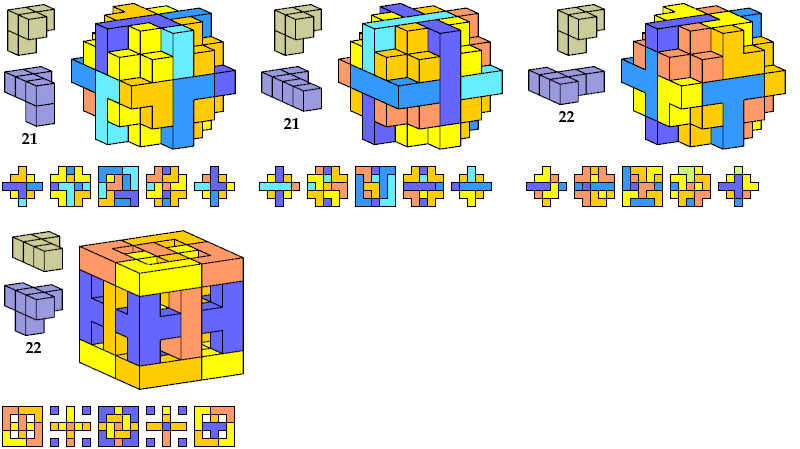
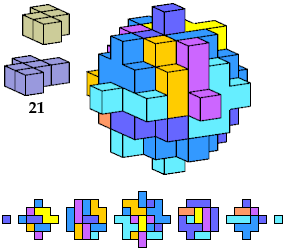
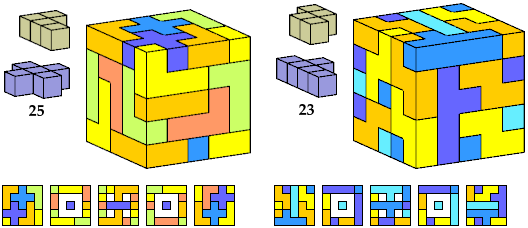


Last revised 2023-02-10.