Pentacube Pair Boxes

Introduction

A pentacube is a solid made of 5 equal cubes joined face to face. There are 29 pentacubes, distinguishing mirror images.

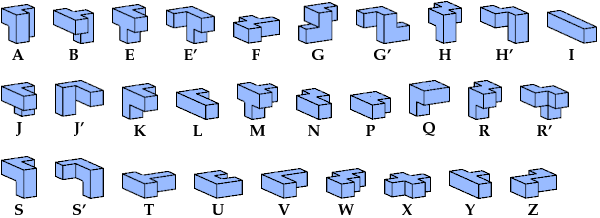
I indicate mirror images with a prime mark (′). For example, S′ denotes the mirror image of pentacube S.

All but two of the pentacubes, G and X, can tile a rectangular prism, or box. All but one pair of pentacubes, G-G′, can jointly tile a box.

Here I show the smallest box known to be tilable with each pair of pentacubes, using at least one copy of each pentacube in the pair. If you find a solution smaller than one shown, or solve an unsolved case, please write.

Tile Counts

Click on an entry in the table to see the corresponding tiling.

	A	B	E	E′	F	G	G′	H	H′	I	J	J′	K	L	M	N	P	Q	R	R′	S	S′	T	U	V	W	X	Y	Z
A		6	6		12	24		8		12	6		6	8	6	4	6	4	6		8		6	6	12	12	40	4	6
B			6		12	14		6		8	4		8	8	10	8	6	6	10		8		15	6	8	12	10	6	12
E				4	6	6	16	4	4	6	6	6	6	4	6	8	4	4	8	6	8	8	12	6	9	8	18	8	6
F						18		8		9	8		8	4	12	8	6	6	12		8		16	6	4	12	40	5	9
G							×	8	8	24	12	4	12	8	48	8	6	6	54	40	24	8	18	12	8	18	200	8	32
H									10	6	8	8	6	4	6	8	4	4	6	8	6	8	8	8	8	6	14	8	6
I											10		12	3	12	8	3	6	12		12		9	6	6	9	9	6	9
J												6	8	4	10	4	6	4	4	6	6	8	6	6	6	8	6	8	6
K														8	4	4	6	4	4		12		16	6	12	6	8	4	6
L															8	4	3	4	8		8		9	4	4	4	5	8	8
M																12	6	6	30		8		8	6	16	12	10	6	8
N																	4	4	8		6		8	4	4	8	16	6	8
P																		4	6		6		3	4	3	4	5	3	3
Q																			6		4		6	4	6	8	6	4	6
R																				28	6	8	8	6	6	12	10	6	12
S																						18	12	6	12	6	15	8	6
T																								6	12	12	63	4	18
U																									8	16	3	6	9
V																										12	24	12	3
W																											36	8	12
X																												5	63
Y																													5
Z

Impossible Case

G and G′ cannot tile even one edge of a box, much less a whole box.

Last revised 2024-02-12.

Back to Polyform Tiling < Polyform Curiosities

Col. George Sicherman [ HOME | MAIL ]