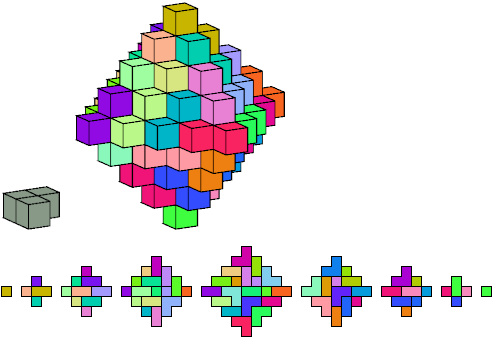
In December 2015 I sent Andy Liu this Christmas tree ornament
consisting of a solid diamond of order 5 dissected into 43 right tricubes:

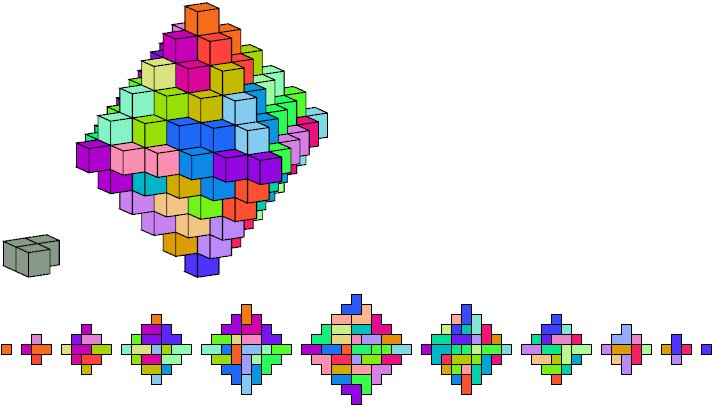
In February 2016 Xin Li sent me this solid diamond of order 6 dissected into 77 right tricubes:
For what other values of n can the solid diamond of order n be tiled with right tricubes? Andy Liu has shown by algebra that the number of cells in a solid diamond of order n is a multiple of 3 if and only if n is congruent to 4, 5, or 6 (mod 9). To show that the solid diamond of order 4 cannot be tiled with right tricubes, color its 63 cells alternately blue and red:
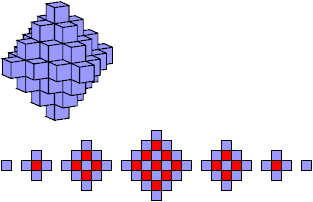
This coloring has 44 blue cells and 19 red cells. But 21 tricubes must contain at least 21 red cells. Therefore 21 right tricubes cannot tile a solid diamond of order 4.
For larger admissible values of n (13, 14, 15, 22, 23, 24, … ) the problem is unsolved. It seems likely that solutions exist for these values of n, but it is not practicable to search by brute force, and no systematic construction is known.
Little is known about m-dimensional analogues of the solid diamond. In 2 dimensions there are no solutions, because the area of a diamond cannot be a multiple of 3. This also holds in 6 and 8 dimensions. In 4 dimensions the value of n may be congruent to 2, 4, 5, 6, or 8 (mod 9). The lowest such value that is not eliminated by the coloring argument is 8, with 2241 cells, 1408 blue and 833 red. Tiling with right trihypercubes is even harder than tiling with right tricubes!
Last revised 2016-02-29.