Polycube Prisms

An old problem in combinatorial geometry is to find the smallest solid box that a polycube can tile. See, for example, Pentacubes in a Box.

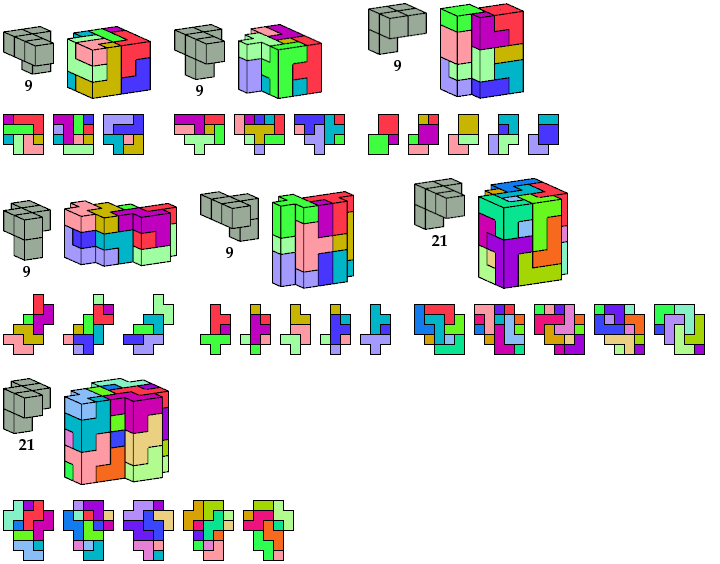
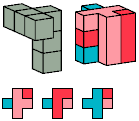
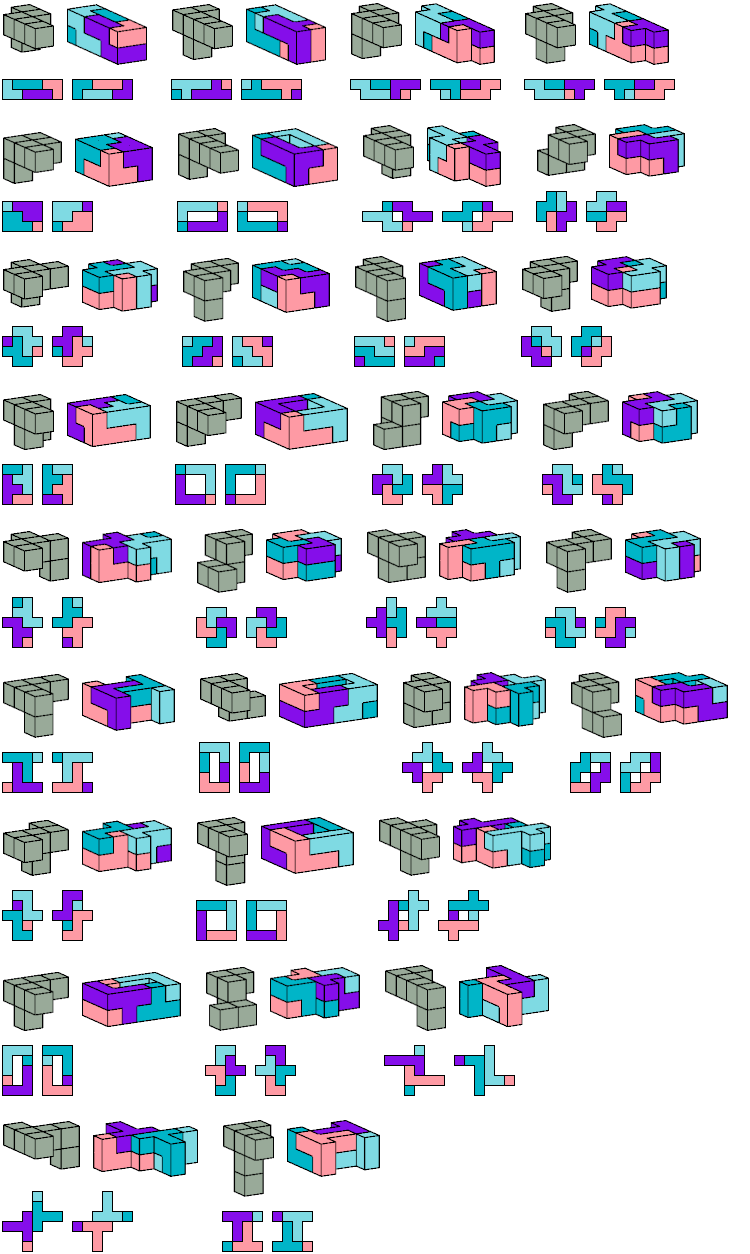
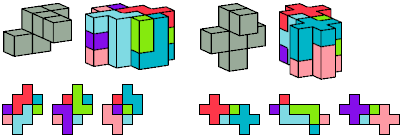
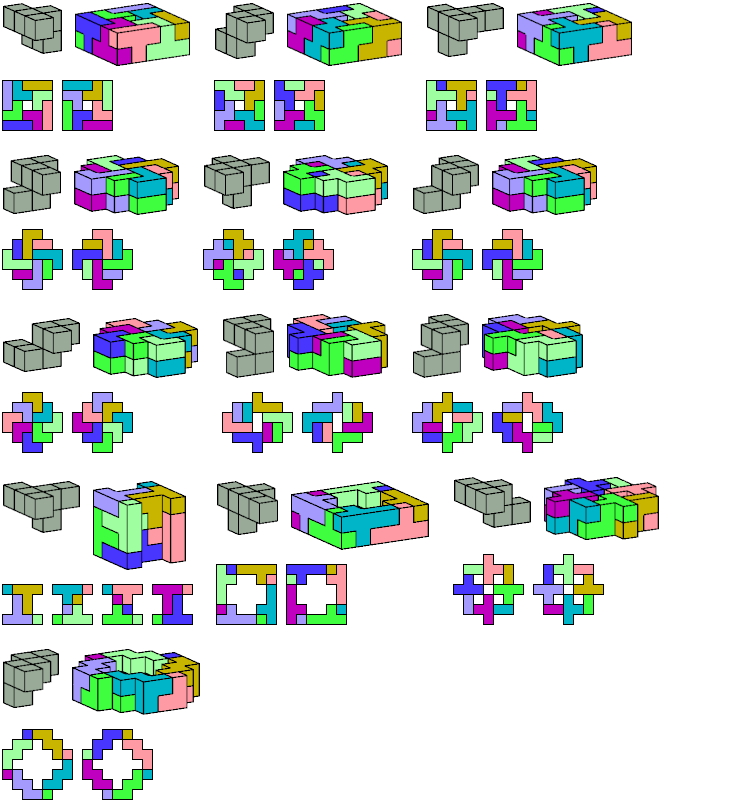
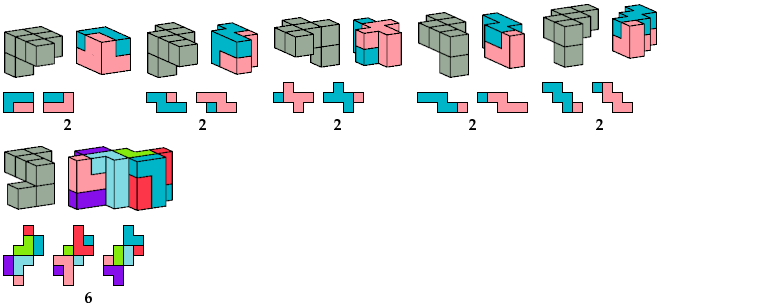
Here I show minimal results for a broader problem: find the smallest prism that a polycube can tile. Some polycubes that cannot tile boxes can tile prisms.

I do not show flat polycubes, which are prisms in their own right.

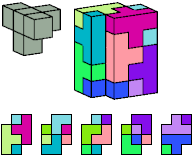
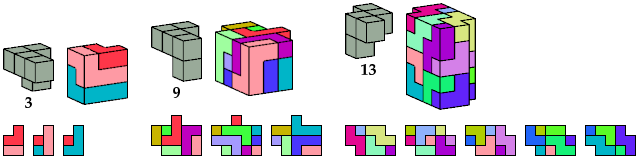
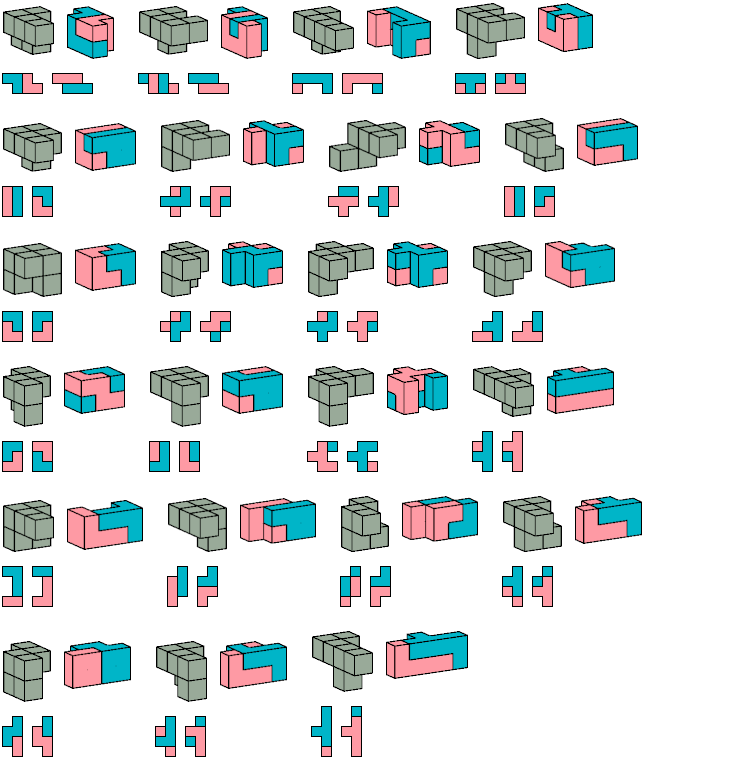
The usual definition of a prism is a solid of uniform height over a polygonal base. Here the polygon is a polyomino. I allow polyominoes with holes, though such polyominoes are technically not polygons.

[ Tetracubes | Pentacubes | Hexacubes ]

Tetracubes

Odd Variant

Pentacubes

Holeless Variant

Odd Variants

These prisms have odd numbers of tiles.

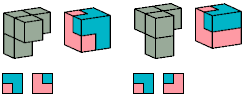
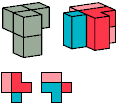
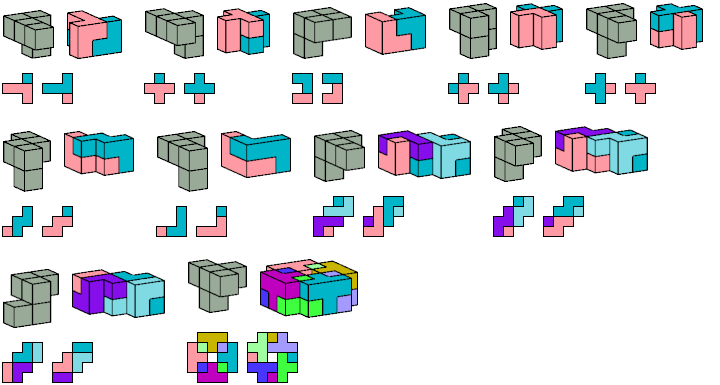
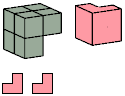
The S pentacube can tile a rectangular prism with dimensions 5×9×15; see Shirakawa's Box Packing Collection.

If you find an odd variant for another pentacube, please write.

Allowing Reflection

Hexacubes

1 Tile

2 Tiles

3 Tiles

4 Tiles

6 Tiles

8 Tiles

Impossible

Allowing Reflection

Sometimes we can use fewer tiles by letting the hexacube be reflected:

Last revised 2024-02-24.

Back to Polyform Tiling < Polyform Curiosities
Col. George Sicherman [ HOME | MAIL ]