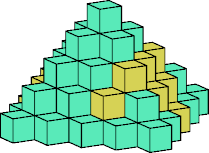
Click on a picture to show the structure of the tiling.
For the two-dimensional counterpart of this problem, see Erich Friedman's Math Magic for May 2006.
[ Quarter Pyramids | Half Pyramids | Full Pyramids | Octahedra ]

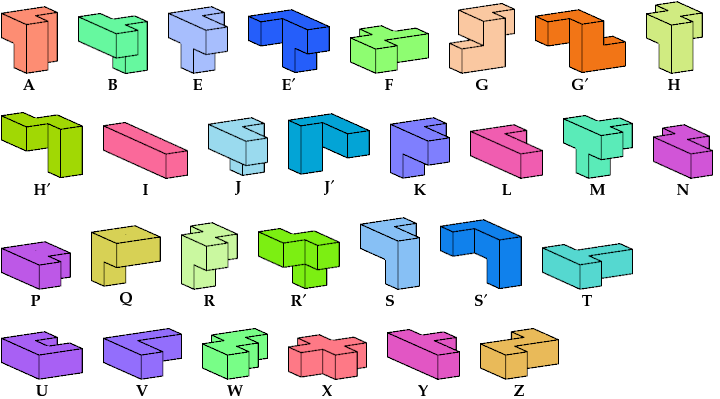
| 5A + 5M | 5A + 5R | 5E + 5H | 5E + 5H′ | 5E + 5R′ | 5E + 5W |
|---|---|---|---|---|---|

| 
| 
| 
| 
| 
|
| 5F + 5H | 5F + 5W | 5H + 5M | 5H + 5R | 5H + 5R′ | 5H + 5W |

| 
| 
| 
| 
| 
|
| 5H + 5Y | 5K + 5M | 5L + 5R | 5L + 5W | 5M + 5P | 5M + 5Q |

| 
| 
| 
| 
| 
|
| 5M + 5W | 5N + 5R | 5N + 5W | 5P + 5Y | 5Q + 5Y | 5R + 5V |

| 
| 
| 
| 
| 
|
| 5R + 5W | 5R + 5Y | 5W + 5Y | |||

| 
| 
|
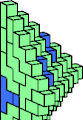
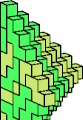
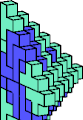
| 5A + 5M | 5E + 5R | 5E + 5W | 5H + 5W | 5J + 5R | 5K + 5M |
|---|---|---|---|---|---|
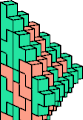
| 
| 
| 
| 
| 
|
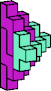
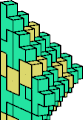
| 5L + 5W | 5M + 5N | 5M + 5Q | 5M + 5U | 5M + 5W | 5R + 5W |
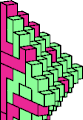
| 
| 
| 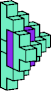
| 
| 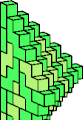
|
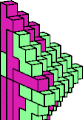
| 5R + 5Y | 5W + 5Y | ||||

| 
|
| 5A + 5M | 5H + 5M | 5M + 5N | 5M + 5P | 5M + 5Q | 5M + 5R |
|---|---|---|---|---|---|

| 
| 
| 
| 
| 
|
| 5M + 5W | 5R + 5X | ||||

| 
|
| 5I + 5M | 5M + 5W | 
| 
|
|---|
Last revised 2019-02-11.