Entangled Polycubes

Introduction

In Issue 74 of Los Acertijeros, Rodolfo Kurchan asked for arrangements of copies of a polyomino in which no single copy can be removed in the plane without moving at least one other copy. He later published results by various contributors in issue 23 of Puzzle Fun.

In the October 2001 issue of Math Magic, Erich Friedman posed the problem of arranging arbitrary polyominoes so that no group of polyominoes could be moved relative to the polyominoes not in the group. He called these Entangled Polyominoes.

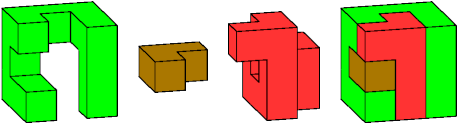
Here is a similar problem for polycubes: for a number n, find the smallest rectangular prism polycube, or box, formed by n polycubes that cannot be separated.

Subtleties

Edo Timmermans has sent me two subtle examples of the difficulty of determining whether polycubes can be separated. In this example, the brown piece can be pulled out easily:

But to separate the red piece from the green piece, we must move the red piece first down one cell, then back one cell, and finally right:

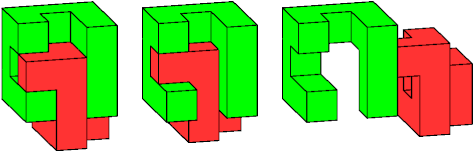
In this example, it is easy to remove the yellow piece:

But then the red piece can be separated from the green piece only by first rotating it around the axis indicated:

Edo is the world's resident expert on polycube tilings. For other remarkable polycube tilings, see his articles in issues 60 and 66 of Cubism for Fun, and this page at Greg Frederickson's website.

See also this entry in Lewis Patterson's blog Polyominoes.

Solutions

Most of the known results for entangled polycubes were found by Yoshiyuki Kotani (小谷善行).

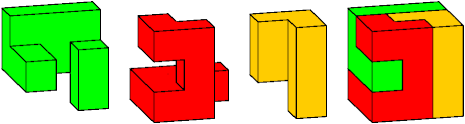
Most of the minimal solutions use the G pentacube:

Two Pieces

Professor Kotani found the smallest box that can be formed by 2 polycubes that cannot be separated. Its dimensions are 2×2×3:

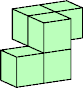
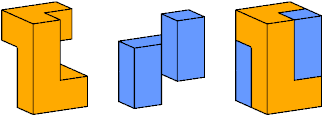
This tiling is the only inseparable tiling of this box.

Three Pieces

Professor Kotani also found the smallest box that can be formed by 3 polycubes that cannot be separated. Its dimensions are 2×3×3:

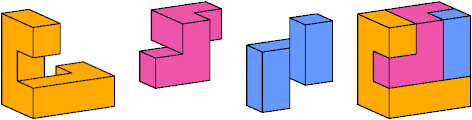
I believe that this tiling is also unique.

Four Pieces

For 4 polycubes, the box with the smallest dimensions is 3×3×3. Professor Kotani gives this solution:

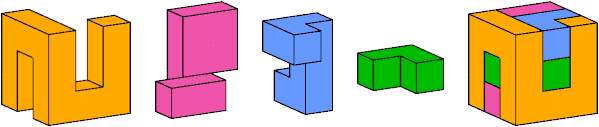
It is not unique. In fact, Professor Kotani points out that one cell of the pink piece may be transferred to the blue piece.

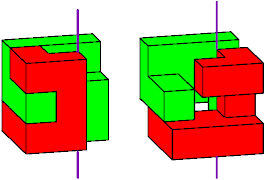
The smallest polycube need not have 3 cells. In this tiling, the smallest polycube has only 1 cell, at the center:

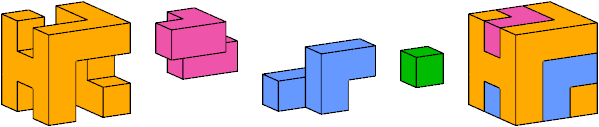
The smallest box by volume with 4 inseparable polycubes is 2×3×4:

I believe that this tiling is unique. Here is a model of it that I made from wooden cubes, glue, and paint:

Five Pieces

A box with dimensions 2×4×4 can be dissected into 5 polycubes that cannot be separated:

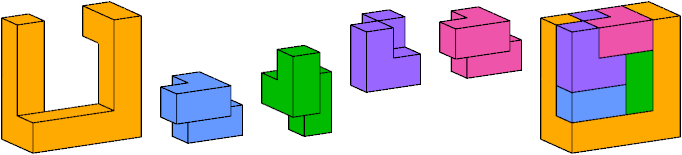
This tiling is not unique.

Last revised 2022-10-05.

Back to Polyform Tiling < Polyform Curiosities
Col. George Sicherman [ HOME | MAIL ]