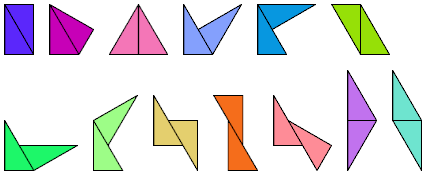
Inflated Didrafters
A didrafter is a polyform
made by joining two drafters,
30°-60°-90° right triangles,
at their short legs, long legs, hypotenuses, or half hypotenuses.
Polydrafters joined on the polyiamond (triangle) grid
are called proper polydrafters.
Polydrafters whose cells depart from the grid are called extended
polydrafters.
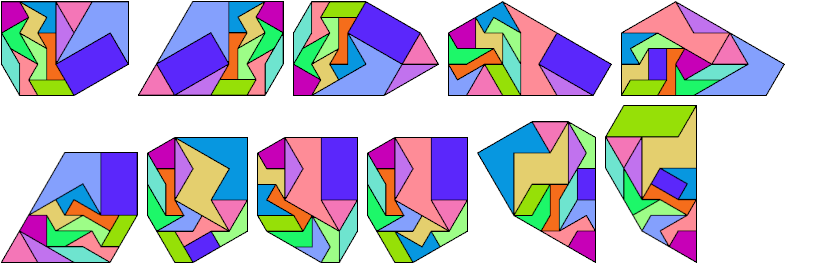
Here are the 13 didrafters, proper and extended:
In 1994 Rodolfo Kurchan introduced inflated pentominoes.
These were rectangular arrangements of the 12 pentominoes, in which some
pentominoes were scaled up by an integer factor.
Here I show convex arrangements of the 13 didrafters,
in which some didrafters are scaled up by an integer factor or √3
times an integer factor.
See also Convex
Shapes from the 13 Didrafters.
Symmetric shapes are marked with an asterisk (*).
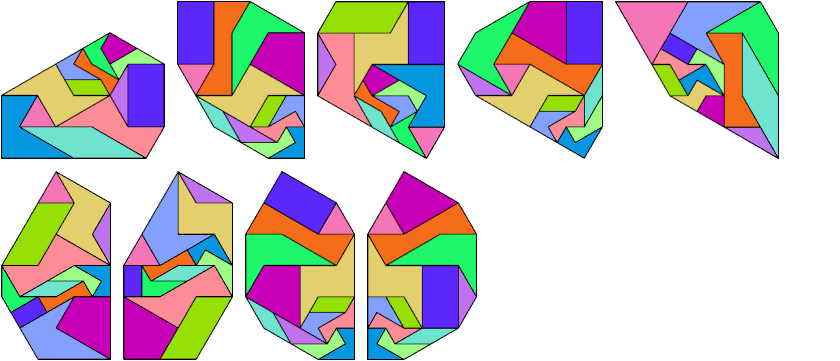
Only one tiling is given for each combination of a convex shape
and an assignment of scales to the tiles.
Patrick Hamlyn tiled two rectangles.
12 @1, 1 @√3
15 tile equivalents.
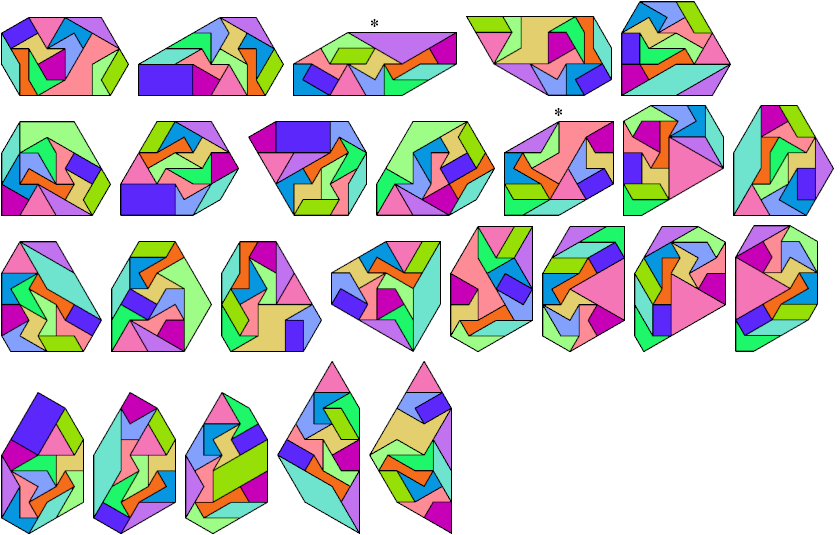
12 @1, 1 @2
16 tile equivalents.
11 @1, 2 @√3
17 tile equivalents.

11 @1, 1 @√3, 1 @2
18 tile equivalents.
10 @1, 3 @√3
19 tile equivalents.

11 @1, 2 @2
19 tile equivalents.
10 @1, 2 @√3, 1 @2
20 tile equivalents.
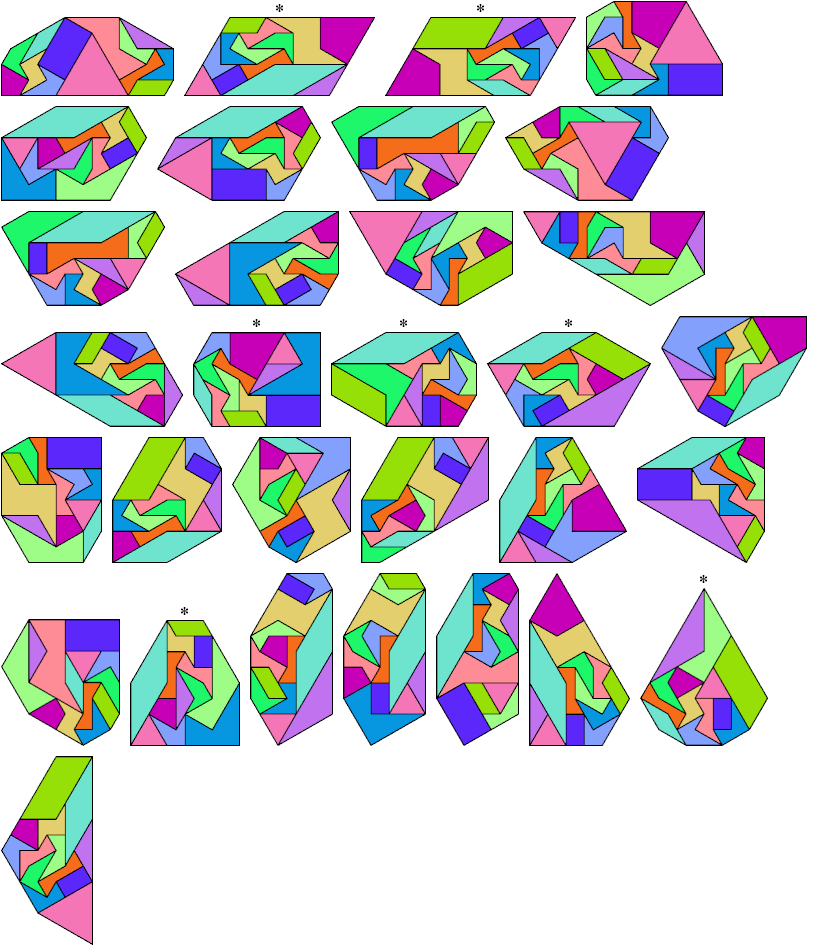
8 @1, 4 @√3, 1 @2
24 tile equivalents. This list is not complete.

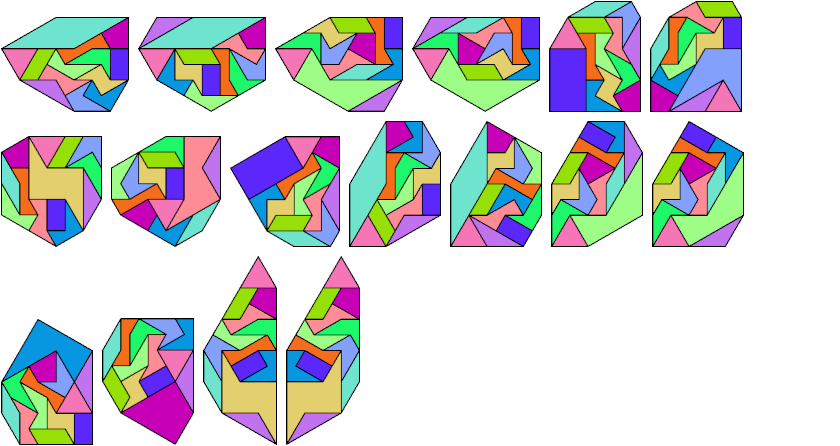
7 @1, 3 @√3, 3 @2
28 tile equivalents.
This list is not complete.
8 @1, 5 @2
28 tile equivalents.
This list is not complete.
6 @1, 6 @√3, 1 @2
28 tile equivalents.
This list is not complete.
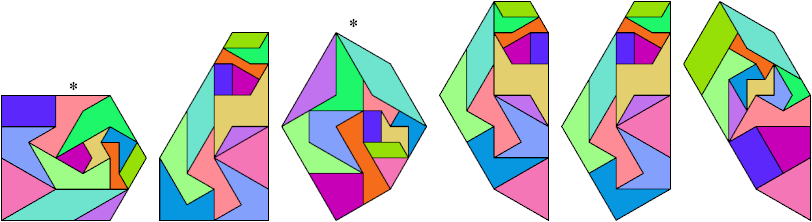
9 @1, 2 @√3, 1 @2, 1 @3
28 tile equivalents.
This list is not complete.
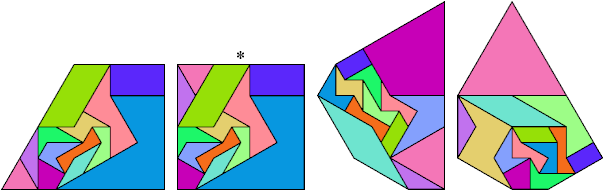
1 @1, 1 @√3, 11 @2
48 tile equivalents.
This list is not complete.
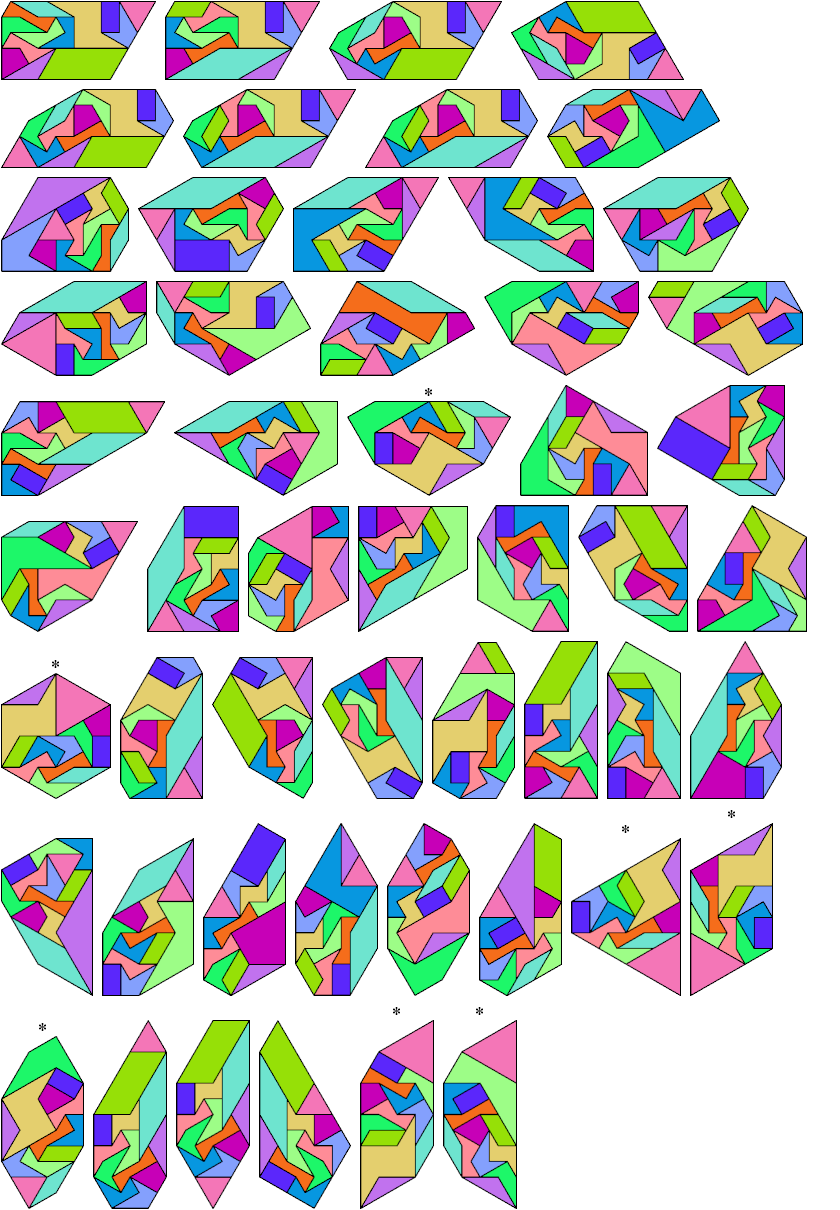
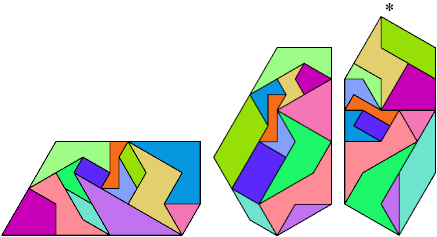
Patrick Hamlyn found the rectangular tiling.
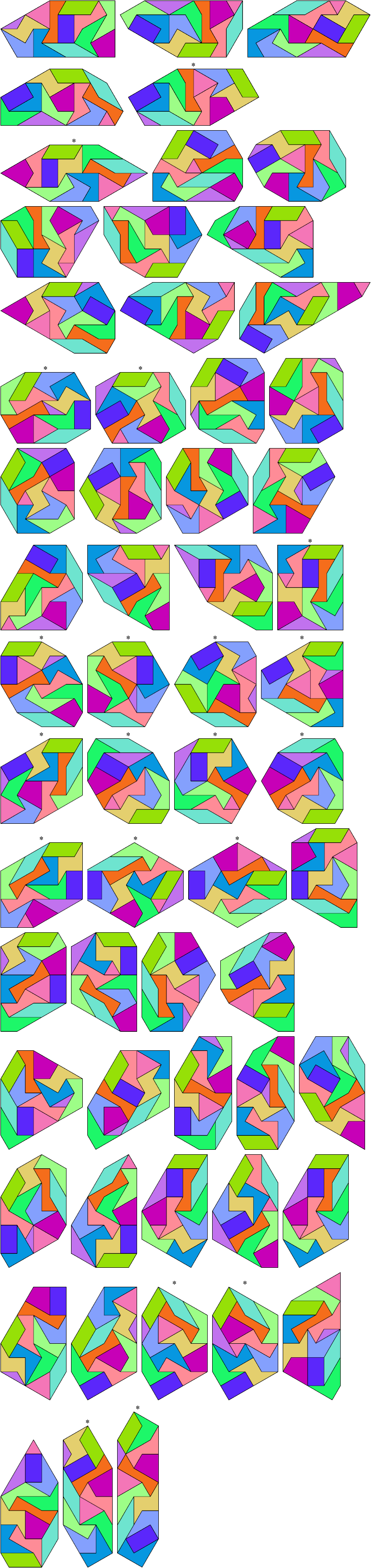
1 @1, 1 @√3, 10 @2, 1 @2√3
56 tile equivalents.
This list is not complete.
Patrick Hamlyn found the rectangular tiling.

Last revised 2021-07-10.
Back to Polydrafter Tiling
< Polyform Tiling
< Polyform Curiosities
Col. George Sicherman
[ HOME
| MAIL
]















