

A reptiling of a polyform is a dissection of it into two or more equal pieces that are all similar to the original polyform. An irreptiling of a polyform is a dissection of it into pieces that are all similar to the original polyform, but not necessarily of equal size. Some shapes have irreptilings and no reptilings.
For irreptilings of polyforms other than polydrafters, see Erich Friedman's Math Magic for October 2002. For more information about irreptiles, see Karl Scherer's book A Puzzling Journey to the Reptiles and Related Animals.
Here I omit polydrafters that are similar to polydrafters with fewer cells, and I show only solutions with the fewest possible pieces. Polydrafters that are also polyiamonds appear with gray backgrounds. If you find a solution with fewer pieces, or solve an unsolved case, please write.

|  |
| 2 |
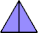
|  |
| 4 | |

| 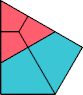 Karl Scherer |
| 5 | |

|  |
| 4 | |

|  |
| 3 | |

|  |
| 4 | |

|  |
| 4 |

|  |
| 4 | |

| 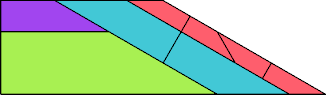 |
| 8 | |
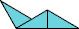
| 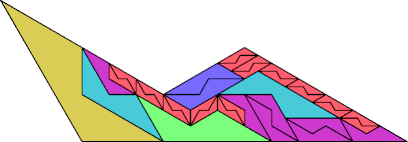 |
| 35 | |

| 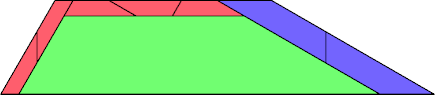 |
| 8 | |

| 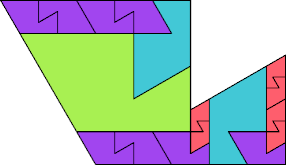 |
| 17 |

|  |
| 4 | |
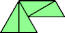
| 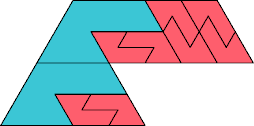 |
| 10 | |

| 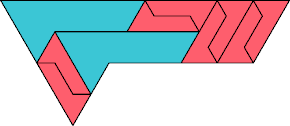 Karl Scherer |
| 10 | |
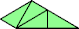
| 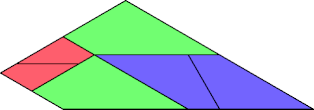 |
| 6 | |

|  |
| 10 | |

|  |
| 3 | |
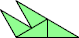
|  |
| 10 | |
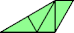
| 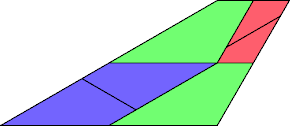 |
| 6 | |

|  |
| 4 | |

|  |
| 4 | |

|  |
| 9 | |

|  |
| 4 | |

|  |
| 4 | |

|  |
| 4 | |
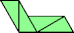
|  |
| 4 |

|  |
| 12 | |

|  |
| 10 | |

| 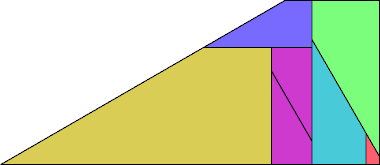 |
| 7 | |

| 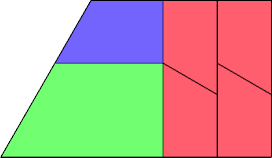 Karl Scherer |
| 6 |

|  |
| 4 | |
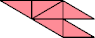
| 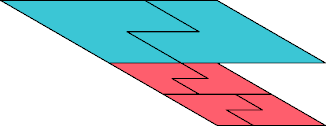 |
| 6 | |
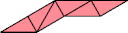
| 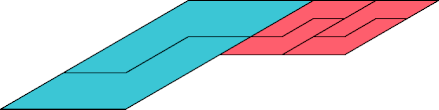 |
| 6 | |
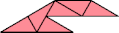
| 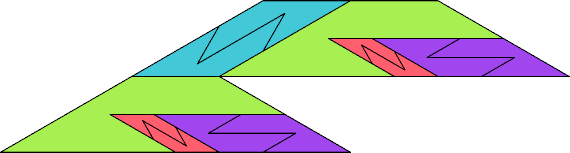 |
| 12 | |

| 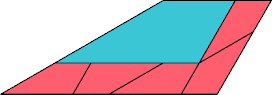 |
| 6 | |

|  |
| 10 | |

|  |
| 4 | |
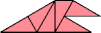
| 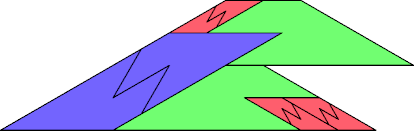 |
| 10 | |
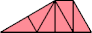
| 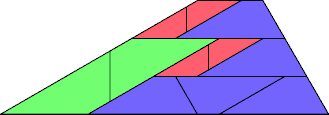 |
| 11 | |

|  |
| 4 | |

| 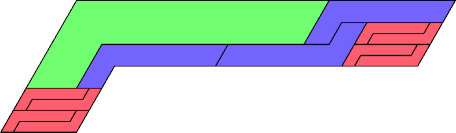 |
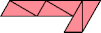
| 12 | |
| 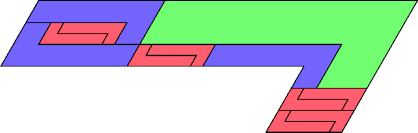 |
| 12 | |

| 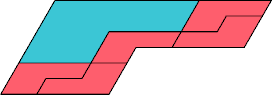 |
| 6 | |
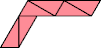
|  |
| 9 | |
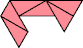
|  |
| 27 | |
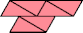
| 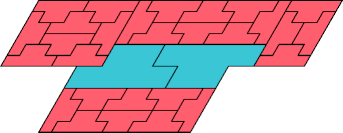 |
| 30 | |
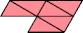
|  |
| 6 | |

|  |
| 27 | |
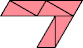
|  |
| 9 | |

| 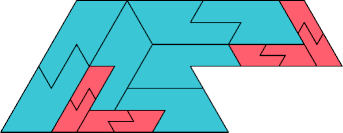 |
| 15 | |

|  |
| 4 | |
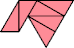
| 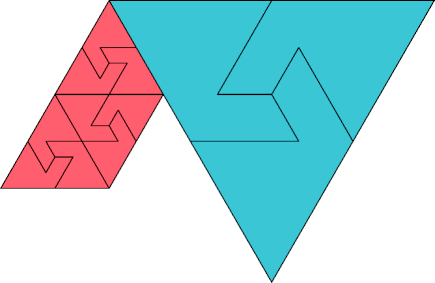 |
| 12 | |
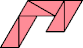
| 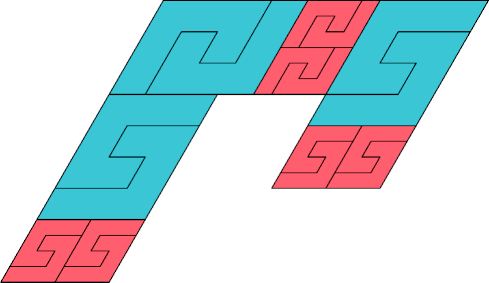 |
| 18 | |

| 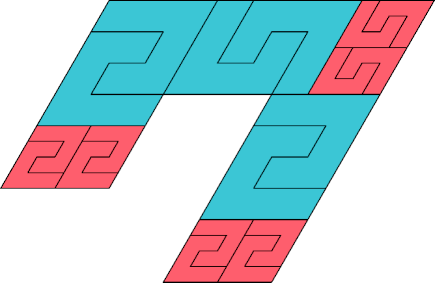 |
| 18 | |

|  |
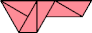
| 4 | |
| 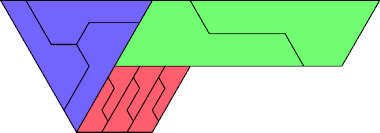 |
| 11 | |

| 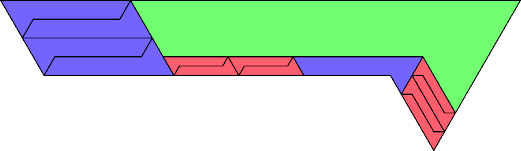 |
| 14 | |

|  |
| 4 | |

|  |
| 4 | |
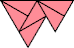
| 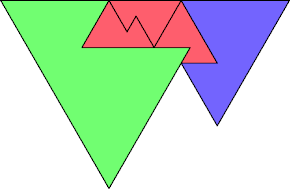 Karl Scherer |
| 5 |
Last revised 2020-08-19.