A prime rectangle for a tetraking is a rectangle that the tetraking can tile, that cannot be tiled by smaller rectangles that the tetraking can tile. Here I show known prime rectangles for the tetrakings that are not also tetrominoes. For prime rectangles for tetrominoes and other polyominoes, see Michael Reid's Rectifiable Polyomino Page.
 | 2×4 8×9 5×16 5×24. |
 | None. |
 | 2×4 8×9 5×16 5×72 7×24. |
 | 2×4. |
 |
14×36
14×48
14×60
18×36
18×48
18×52
18×56
18×60
18×64
18×68
18×76
18×80
19×48
19×72
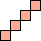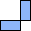
20×30 20×36 20×42 20×48 20×54 21×32 21×40 21×48 21×56 22×36 22×48 22×60 23×48 23×72 24×28 24×30 24×32 24×33 24×34 24×35 24×36 24×37 24×38 24×39 24×40 24×41 24×42 24×43 24×44 24×45 24×46 24×47 24×48 24×49 24×50 24×51 24×52 24×53 24×54 24×55 24×57 24×59 25×48 25×72 26×36 26×48 26×60 27×32 27×40 27×48 27×56 28×30 28×42 29×48 29×72 30×32 30×36 31×48 31×72 32×33 32×39 33×40 39×40. Completed by Toshihiro Shirakawa, 2015. |
 | 4×4 8×10 8×13 8×19 10×20 11×16 11×24 12×14. |
 |
8×12
8×15
8×16
8×18
8×19
8×20
8×21
8×22
8×23
8×25
8×26
8×29
9×16
9×24
10×12
10×16
10×20
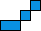
11×16 11×24 12×12 12×14 13×16 13×24 14×16 14×20. Completed by Toshihiro Shirakawa, 2015. |
 | 2×4 7×8. |
 | 2×4. |
 | 4×4. |
 | 2×4. |
 | None. |
 | None. |
 | None. |
 | None. |
 | None. |
 | None. |
Last revised 2017-10-11.
