Pentiamond-Hexiamond Oddities
A polyiamond oddity
is a figure with binary symmetry formed by an odd number of copies of
a polyiamond.
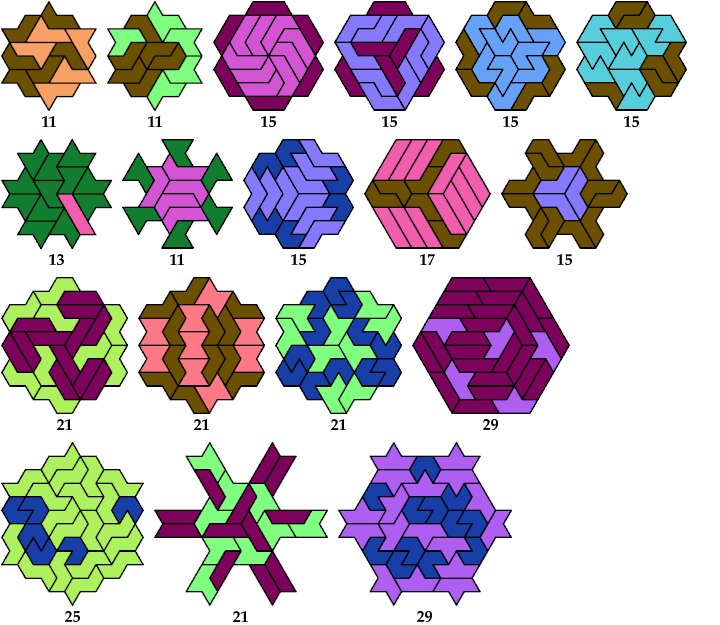
Here are the minimal known oddities for pentiamond-hexiamond pairs.
In Tetromino-Pentomino Oddities
I used figures with an odd number of cells.
Unlike polyominoes, a polyiamond with full symmetry cannot have an odd number
of cells.
Here I use figures with an odd number of tiles instead.
Johann Schwenke and Carl Schwenke contributed many solutions.
[ Basic Solutions
| Holeless Variants
]
| 5I+6A : 17 | 5J+6A : 17 | 5Q+6A : 13 | 5U+6A : 7 |
 |  |  |  |
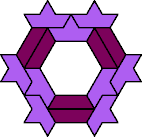
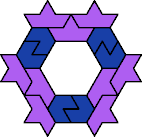
| 5I+6E : 15 | 5J+6E : 11 | 5Q+6E : 13 | 5U+6E : 15 |
 |  |  |  |
| 5I+6F : 9 | 5J+6F : 9 | 5Q+6F : 13 | 5U+6F : 9 |
 |  |  |  |
| 5I+6H : 9 | 5J+6H : 9 | 5Q+6H : 13 | 5U+6H : 9 |
 |  |  |  |
| 5I+6I : 15 | 5J+6I : 9 | 5Q+6I : 9 | 5U+6I : 15 |
 |  |  |  |
| 5I+6L : 9 | 5J+6L : 9 | 5Q+6L : 9 | 5U+6L : 15 |
 |  |  |  |
| 5I+6O : 9 | 5J+6O : 9 | 5Q+6O : 7 | 5U+6O : 7 |
 |  |  |  |
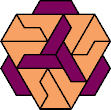
| 5I+6P : 15 | 5J+6P : 9 | 5Q+6P : 11 | 5U+6P : 15 |
 |  |  |  |
| 5I+6S : 15 | 5J+6S : 11 | 5Q+6S : 9 | 5U+6S : 19 |
 |  |  |  |
| 5I+6U : 15 | 5J+6U : 9 | 5Q+6U : 9 | 5U+6U : 9 |
 |  |  |  |
| 5I+6V : 9 | 5J+6V : 9 | 5Q+6V : 9 | 5U+6V : 9 |
 |  |  |  |
| 5I+6X : 11 | 5J+6X : 15 | 5Q+6X : 13 | 5U+6X : 9 |
 |  |  |  |
Unsolved

Last revised 2021-11-23.
Back to Polyform Oddities
<
Polyform Curiosities
Col. George Sicherman
[ HOME
| MAIL
]

















































