Tiling a Shape with Ternary Symmetry with
the Heptiamonds and the Tetrahexes
Introduction
A heptiamond is a figure made of seven equilateral triangles joined
edge to edge.
There are 24 such figures, not distinguishing reflections and rotations.
The nomenclature is taken from K. Ishino.
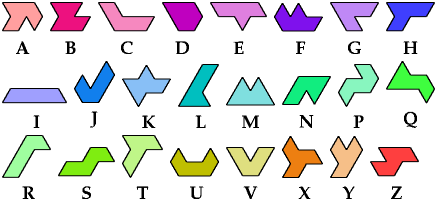
A tetrahex is a figure made of four regular hexagons joined edge
to edge.
There are 7 such figures, not distinguishing reflections and rotations.

Todor Tchervenkov has defined
bi-tileability
as the ability to tile a shape with either of two sets of tiles.
At this page
he presents some results in bi-tileability using polyiamonds and polyhexes.
Heptiamonds and Tetrahexes
If we identify the monohex with the hexagonal hexiamond, the 24 heptiamonds
have the same area as the 7 tetrahexes: 168 iamond cells.
This suggests that some shapes can be tiled with the heptiamonds
and with the tetrahexes.
See Tchervenkov's page for general examples.
The general problem of tiling a shape with the heptiamonds
and with the tetrahexes has too many solutions to present.
Tchervenkov has reduced the problem by adding conditions of
symmetry, large holes, or numerous holes.
Ternary Symmetry
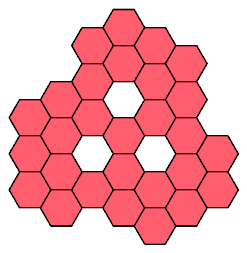
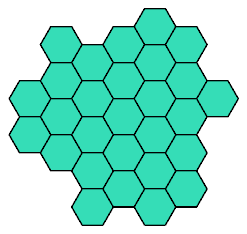
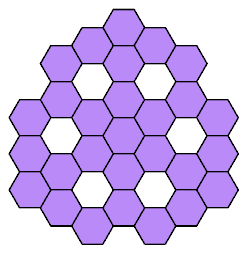
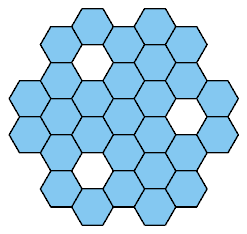
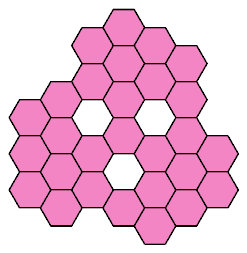
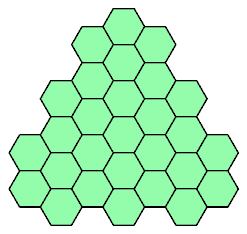
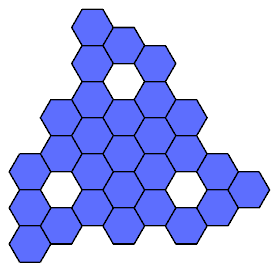
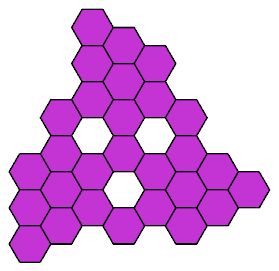
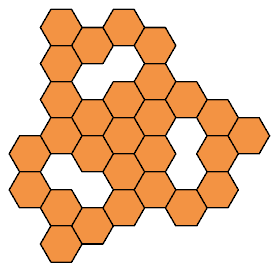
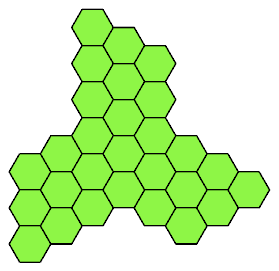
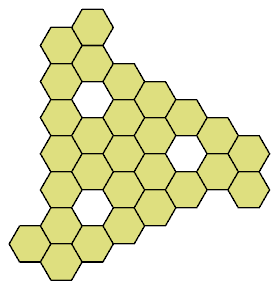
Here I present all such shapes that have ternary (3-way) symmetry.
Some also have mirror symmetry.
Click on a 28-hex to see its tilings by the heptiamonds and the tetrahexes.
The tilings are not necessarily unique.
Last revised 2020-10-10.
Back to Polyform Tiling
<
Polyform Curiosities
Col. George Sicherman
[ HOME
| MAIL
]


