Two-Pentomino Balanced Rectangles

  • Introduction
  • Nomenclature
  • Table
  • Minimal Solutions
  • Contiguous Variants
  • Square Solutions

    • Introduction

    A pentomino is a figure made of five squares joined edge to edge. There are 12 such figures, not distinguishing reflections and rotations. They were first enumerated and studied by Solomon Golomb.

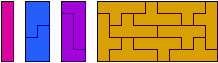
    It has long been known that only four pentominoes can tile rectangles:

    For other rectangles that these pentominoes tile, see Mike Reid's Rectifiable Polyomino Page.

    Rodolfo Kurchan's online magazine Puzzle Fun studied the problem of tiling some rectangle with two different pentominoes, in Issue 19, and revisited the problem in Issue 21. The August 2010 issue of Erich Friedman's Math Magic broadened this problem to use two polyominoes of any size, not necessarily the same.

    Here I study the related problem of tiling some rectangle with two pentominoes, using the same number of copies of each.

    For other sizes of polyominoes, see issue 26 of Puzzle Fun.

    Nomenclature

    I use Solomon W. Golomb's original names for the pentominoes:

    Table

    This table shows the smallest total number of pentominoes known to be able to tile a rectangle in equal numbers.

    FILNPTUVWXYZ
    F * 28 4 × 8 × 12 4 × × 8 ×
    I 28 * 4 24 4 56 ? 12 56 ? 8 60
    L 4 4 * 4 4 24 4 4 4 ? 8 32
    N × 24 4 * 4 24 4 4 × × 8 ×
    P 8 4 4 4 * 12 4 6 8 40 4 12
    T × 56 24 24 12 * 96 × 64 × 4 ×
    U 12 ? 4 4 4 96 * 136 × × 12 ×
    V 4 12 4 4 6 × 136 * 72 × 12 4
    W × 56 4 × 8 64 × 72 * × 14 ×
    X × ? ? × 40 × × × × * 20 ×
    Y 8 8 8 8 4 4 12 12 14 20 * 8
    Z × 60 32 × 12 × × 4 × × 8 *

    Solutions

    So far as I know, these solutions have minimal area. They are not necessarily uniquely minimal.

    4 Tiles

    6 Tiles

    8 Tiles

    12 Tiles

    14 Tiles

    20 Tiles

    24 Tiles

    28 Tiles

    32 Tiles

    40 Tiles

    56 Tiles

    60 Tiles

    64 Tiles

    72 Tiles

    96 Tiles

    136 Tiles

    Contiguous Variants

    Square Solutions

    20 Tiles

    80 Tiles

    180 Tiles

    Contiguous Variants

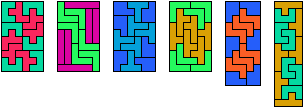
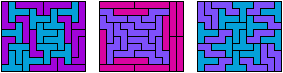
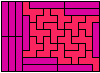
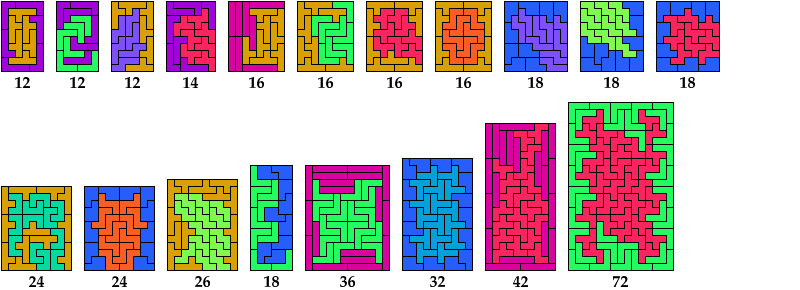
    Last revised 2023-07-24.

    Back to Polyform Tiling < Polyform Curiosities
    Col. George Sicherman [ HOME | MAIL ]