Scaled Three-Pentomino Balanced Rectangles

Introduction

A pentomino is a figure made of five squares joined edge to edge. There are 12 such figures, not distinguishing reflections and rotations. They were first enumerated and studied by Solomon Golomb.

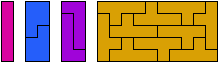
It has long been known that only four pentominoes can tile rectangles:

For other rectangles that these pentominoes tile, see Mike Reid's Rectifiable Polyomino Page.

On Balanced Three-Pentomino Rectangles I study the related problem of tiling some rectangle with three pentominoes, using the same areas of each. Here I study the same problem, using the pentominoes in various sizes. If you find a solution better than one of mine, or solve an unsolved case, please write!

Bryce Herdt improved on some of my solutions.

See also Scaled Two-Pentomino Balanced Rectangles.

Nomenclature

I use Solomon W. Golomb's original names for the pentominoes:

Solutions

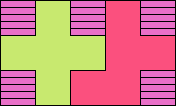
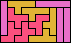
5F+5I+5L 65F+5I+5N 165F+5I+5P 95F+5I+5T 135F+5I+5U 6
5F+5I+5V 65F+5I+5W 155F+5I+5X 275F+5I+5Y 125F+5I+5Z 15
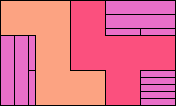
5F+5L+5N 65F+5L+5P 65F+5L+5T 65F+5L+5U 65F+5L+5V 6
5F+5L+5W 65F+5L+5X 305F+5L+5Y 95F+5L+5Z 125F+5N+5P 12
5F+5N+5T 185F+5N+5U 65F+5N+5V 65F+5N+5W ×5F+5N+5X ×
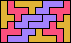
5F+5N+5Y 125F+5N+5Z ×5F+5P+5T 125F+5P+5U 35F+5P+5V 6
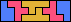
5F+5P+5W 125F+5P+5X 305F+5P+5Y 65F+5P+5Z 185F+5T+5U 18
5F+5T+5V 245F+5T+5W 245F+5T+5X ×5F+5T+5Y 65F+5T+5Z ×
5F+5U+5V 95F+5U+5W 65F+5U+5X 355F+5U+5Y 125F+5U+5Z 19
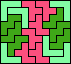
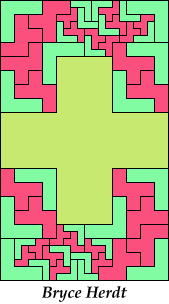
5F+5V+5W 185F+5V+5X 575F+5V+5Y 125F+5V+5Z 125F+5W+5X ×
5F+5W+5Y 125F+5W+5Z ×5F+5X+5Y 245F+5X+5Z ×5F+5Y+5Z 12
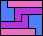
5I+5L+5N 65I+5L+5P 65I+5L+5T 125I+5L+5U 65I+5L+5V 6
5I+5L+5W 65I+5L+5X 205I+5L+5Y 65I+5L+5Z 95I+5N+5P 6
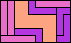
5I+5N+5T 65I+5N+5U 65I+5N+5V 65I+5N+5W 155I+5N+5X 30
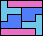
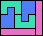
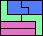
5I+5N+5Y 65I+5N+5Z 125I+5P+5T 65I+5P+5U 65I+5P+5V 6
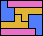
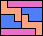
5I+5P+5W 95I+5P+5X 155I+5P+5Y 65I+5P+5Z 65I+5T+5U 13
5I+5T+5V 95I+5T+5W 125I+5T+5X 205I+5T+5Y 65I+5T+5Z 13
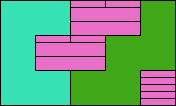
5I+5U+5V 95I+5U+5W 155I+5U+5X 155I+5U+5Y 65I+5U+5Z 15
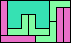
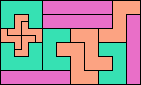
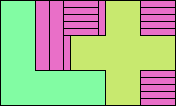
5I+5V+5W 125I+5V+5X 215I+5V+5Y 65I+5V+5Z 65I+5W+5X 21
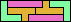
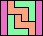
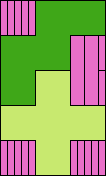
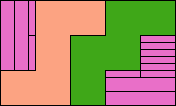
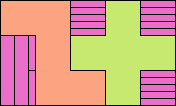
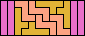
5I+5W+5Y 65I+5W+5Z 155I+5X+5Y 185I+5X+5Z 215I+5Y+5Z 12
5L+5N+5P 65L+5N+5T 125L+5N+5U 65L+5N+5V 35L+5N+5W 6
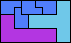
5L+5N+5X 95L+5N+5Y 65L+5N+5Z 65L+5P+5T 65L+5P+5U 6
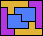
5L+5P+5V 35L+5P+5W 65L+5P+5X 95L+5P+5Y 65L+5P+5Z 6
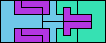
5L+5T+5U 125L+5T+5V 65L+5T+5W 175L+5T+5X 65L+5T+5Y 3
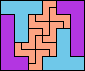
5L+5T+5Z 125L+5U+5V 95L+5U+5W 65L+5U+5X 125L+5U+5Y 6
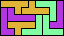
5L+5U+5Z 125L+5V+5W 125L+5V+5X 95L+5V+5Y 95L+5V+5Z 6
5L+5W+5X 365L+5W+5Y 65L+5W+5Z 185L+5X+5Y 185L+5X+5Z 33
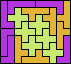
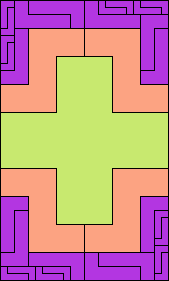
5L+5Y+5Z 65N+5P+5T 65N+5P+5U 35N+5P+5V 65N+5P+5W 12
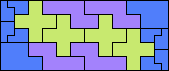
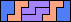
5N+5P+5X 185N+5P+5Y 65N+5P+5Z 65N+5T+5U 125N+5T+5V 9
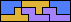
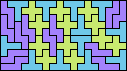
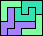
5N+5T+5W 125N+5T+5X 365N+5T+5Y 65N+5T+5Z 245N+5U+5V 6
5N+5U+5W 245N+5U+5X 185N+5U+5Y 65N+5U+5Z 65N+5V+5W 6
5N+5V+5X 555N+5V+5Y 125N+5V+5Z 65N+5W+5X ×5N+5W+5Y 12
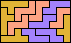
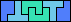
5N+5W+5Z ×5N+5X+5Y 155N+5X+5Z ×5N+5Y+5Z 125P+5T+5U 6
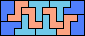
5P+5T+5V 65P+5T+5W 65P+5T+5X 125P+5T+5Y 65P+5T+5Z 12
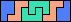
5P+5U+5V 35P+5U+5W 125P+5U+5X 65P+5U+5Y 35P+5U+5Z 6
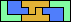
5P+5V+5W 65P+5V+5X 185P+5V+5Y 65P+5V+5Z 65P+5W+5X 30
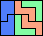
5P+5W+5Y 65P+5W+5Z 65P+5X+5Y 125P+5X+5Z 335P+5Y+5Z 6
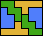
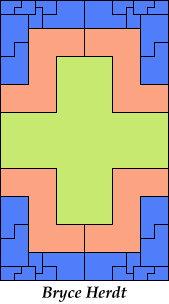
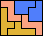
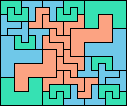
5T+5U+5V 125T+5U+5W 185T+5U+5X 485T+5U+5Y 65T+5U+5Z 36
5T+5V+5W 245T+5V+5X 1215T+5V+5Y 125T+5V+5Z 215T+5W+5X 54
Click here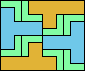
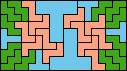
5T+5W+5Y 65T+5W+5Z 305T+5X+5Y 215T+5X+5Z ×5T+5Y+5Z 12
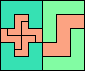
5U+5V+5W 475U+5V+5X 575U+5V+5Y 95U+5V+5Z 95U+5W+5X 60
Click here Click here
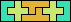
5U+5W+5Y 65U+5W+5Z 185U+5X+5Y 65U+5X+5Z 635U+5Y+5Z 12
Click here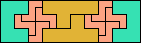
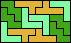
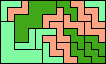
5V+5W+5X 1565V+5W+5Y 125V+5W+5Z 215V+5X+5Y 425V+5X+5Z 9
5V+5Y+5Z 65W+5X+5Y 305W+5X+5Z ×5W+5Y+5Z 125X+5Y+5Z 24

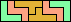
Last revised 2021-06-18.

Back to Polyform Tiling < Polyform Curiosities
Col. George Sicherman [ HOME | MAIL ]