Prime Rectangle Tilings of the Y Pentomino

Introduction

A pentomino is a figure made of five squares joined edge to edge. There are 12 pentominoes, not distinguishing reflections and rotations. They were first enumerated and studied by Solomon Golomb, who named them after letters of the alphabet.

Four pentominoes can tile rectangles: I, L, P, and Y. A rectangle tiled by a polyomino is said to be prime if it cannot be composed of smaller tilable rectangles. Michael Reid's Rectifiable Polyomino Page catalogues prime rectangles for small polyominoes. It shows some examples, including the smallest rectangle for each polyomino.

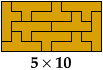
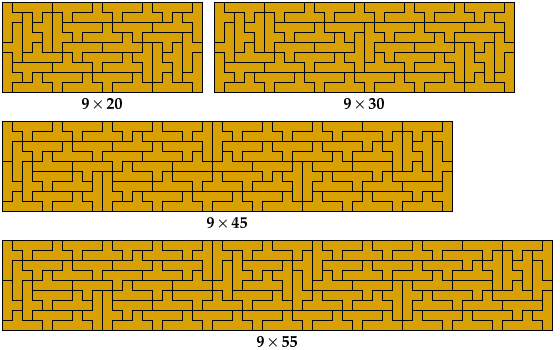
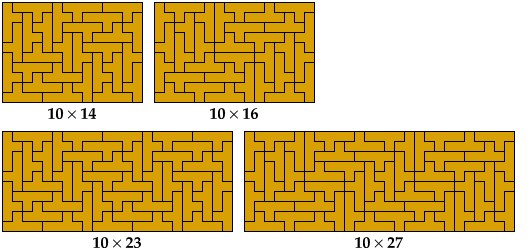
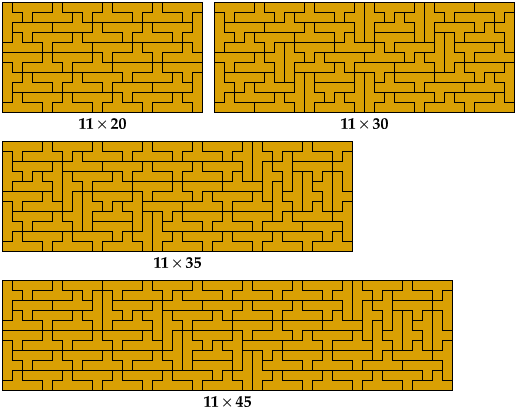
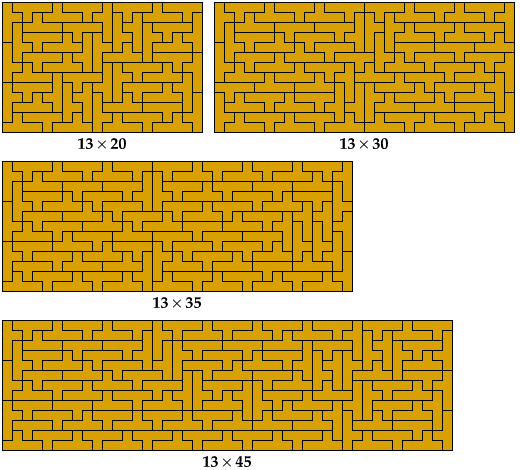
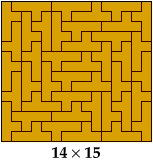
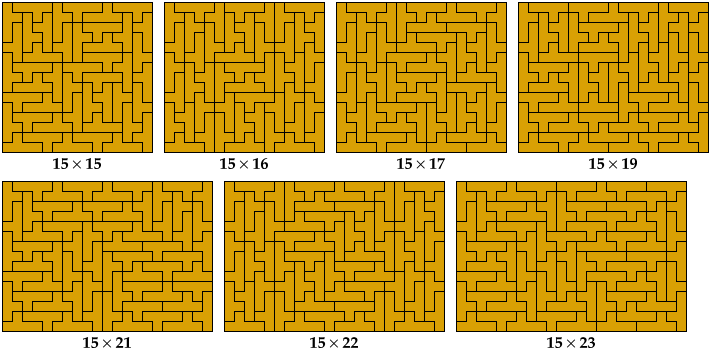
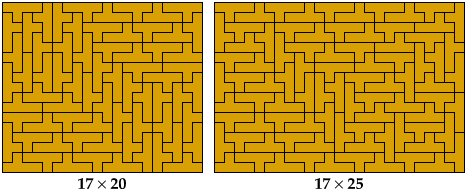
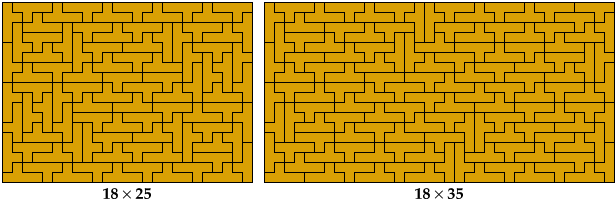
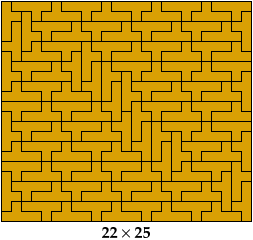
Here are tilings of all 40 prime rectangles for the Y pentomino. The tilings are not unique. They are sorted by their shorter dimension.

The complete set was first identified in 1992 by Torsten Sillke, and first published in 2001, in the Mathematics and Informatics Quarterly, by Julian Fogel, Mark Goldenberg, and Andy Liu, who identified it independently of Sillke.

  • Width 5
  • Width 9
  • Width 10
  • Width 11
  • Width 12
  • Width 13
  • Width 14
  • Width 15
  • Width 17
  • Width 18
  • Width 22

    • Width 5

    Width 9

    Width 10

    Width 11

    Width 12

    Width 13

    Width 14

    Width 15

    Width 17

    Width 18

    Width 22

    Last revised 2018-09-28.

    Back to Polyform Tiling < Polyform Curiosities
    Col. George Sicherman [ HOME | MAIL ]