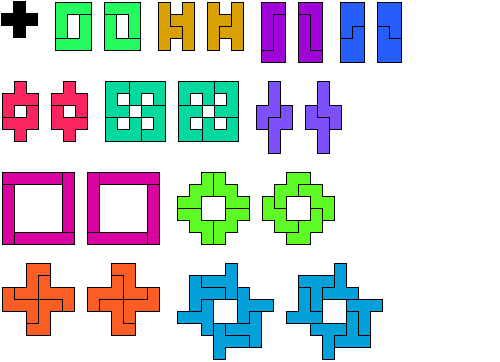
Galvagni Figures & Reid Figures for Pentominoes

A pentomino is a figure made of five squares joined edge to edge. A Galvagni figure is a figure that can be tiled by a polyform in more than one way—a kind of self-compatibility figure. A Reid figure is a Galvagni figure without holes.

Most of the pentomino Galvagni and Reid figures were found by Erich Friedman of Stetson University and Michael Reid of the University of Central Florida. Corey Plover found the minimal Galvagni figure for the T pentomino.

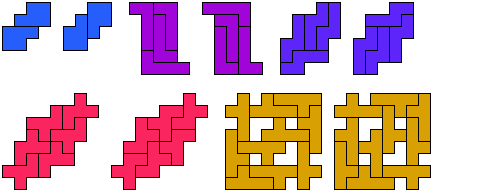
Here are minimal known Galvagni figures for pentominoes. See also Galvagni Figures & Reid Figures for Hexominoes, Galvagni Figures & Reid Figures for Heptominoes, and Galvagni Figures & Reid Figures for Octominoes.

And here are minimal known Reid figures:

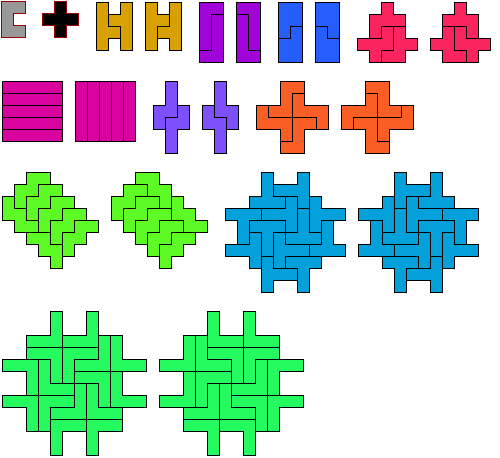
Here is an orthogonally symmetric variant for the W pentomino:

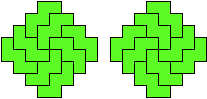
Here are diagonally symmetric variants for the F, L, N, P, and Y pentominoes:

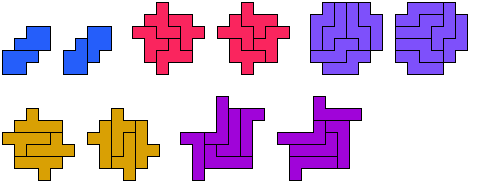
Here is a birotarily symmetric variant for the F pentomino:

Biased Pentominoes

Biased pentominoes may be reflected diagonally and rotated 180° but not 90°.

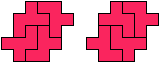
For a discussion of restricted-motion polyominoes, see Alexandre Owen Muñiz's A Polyformist's Toolkit.

Last revised 2014-10-09.

Back to Galvagni Compatibility < Polyform Compatibility < Polyform Curiosities

Col. George Sicherman [ HOME | MAIL ]