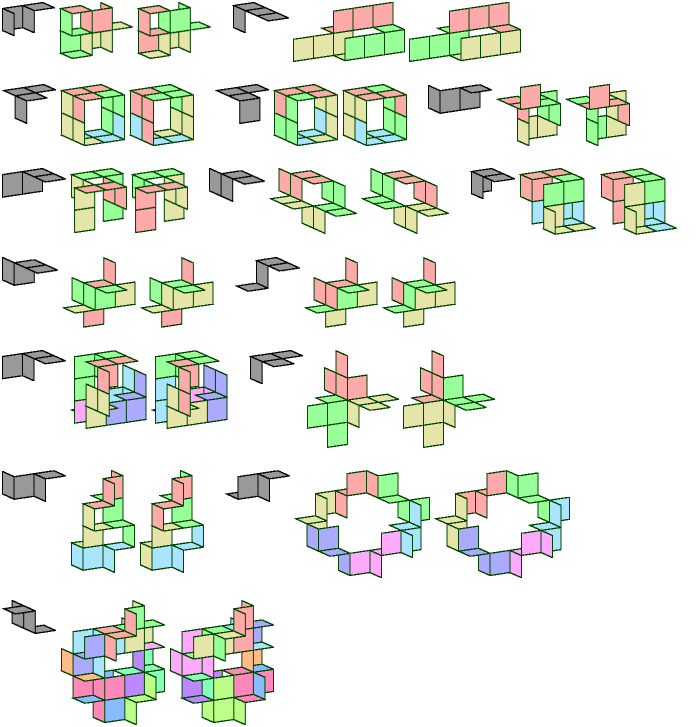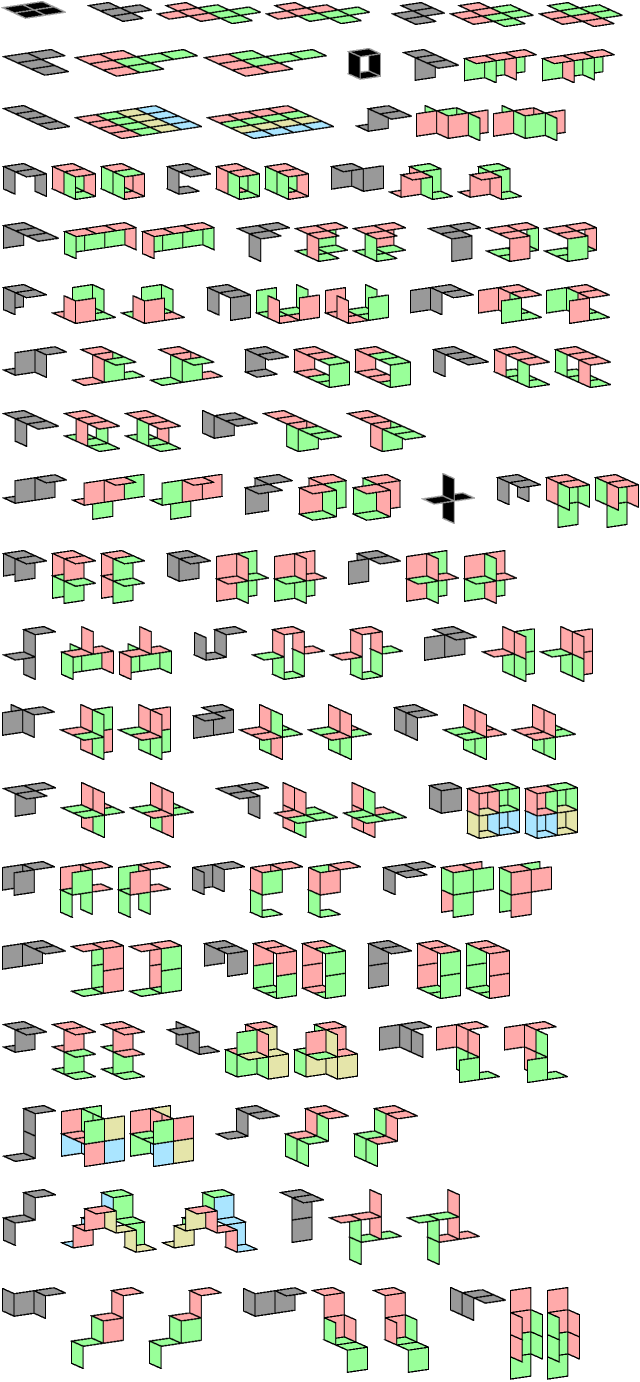
A tetrominoid is formed by joining four squares edge to edge. A Galvagni figure is a figure that can be tiled by a polyform in more than one way—a kind of self-compatibility figure.
There are 54 tetrominoids, or 80 if we count mirror images as distinct. Here are Galvagni figures for 51 of the tetrominoids. The tetrominoids in black have no Galvagni figures.

One of the figures above has two interpenetrating tiles. Here is a three-tile solution without interpenetration.
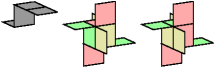
A Plover figure is a Galvagni figure that does not reflect the tile. If a polyform lacks mirror symmetry, its minimal Plover figure may require more tiles than its minimal Galvagni figure.
Here are minimal known Plover figures for tetrominoids without mirror symmetry whose Galvagni figures above are not Plover figures.