Tiling Strips With Polyominoes

Introduction

A polyomino is a figure made of equal squares joined edge to edge. They were first enumerated and studied by Solomon Golomb.

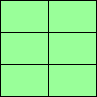
With special reference to strips, Andy Liu defines seven levels of ability to tile strips of cells with a specified polyomino:

The polyomino can tile a rectangle. In this case, it can also tile a square by joining copies of the rectangle:
The polyomino can tile an infinite strip of cells with a 90° bend. It does not matter whether the arms of the strip are required to have the same width. If not, two copies of a strip can be nested to form a strip whose arms have equal width:
The polyomino can tile an infinite straight strip of cells.
The polyomino can tile an infinite straight strip of cells with another straight strip branching off from it.
The polyomino can tile a crossed pair of straight strips.
The polyomino can tile the plane.
The polyomino cannot tile the plane.

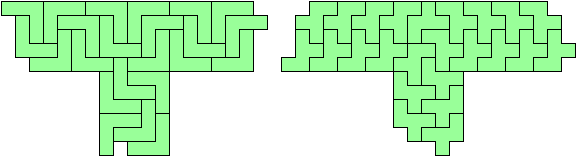
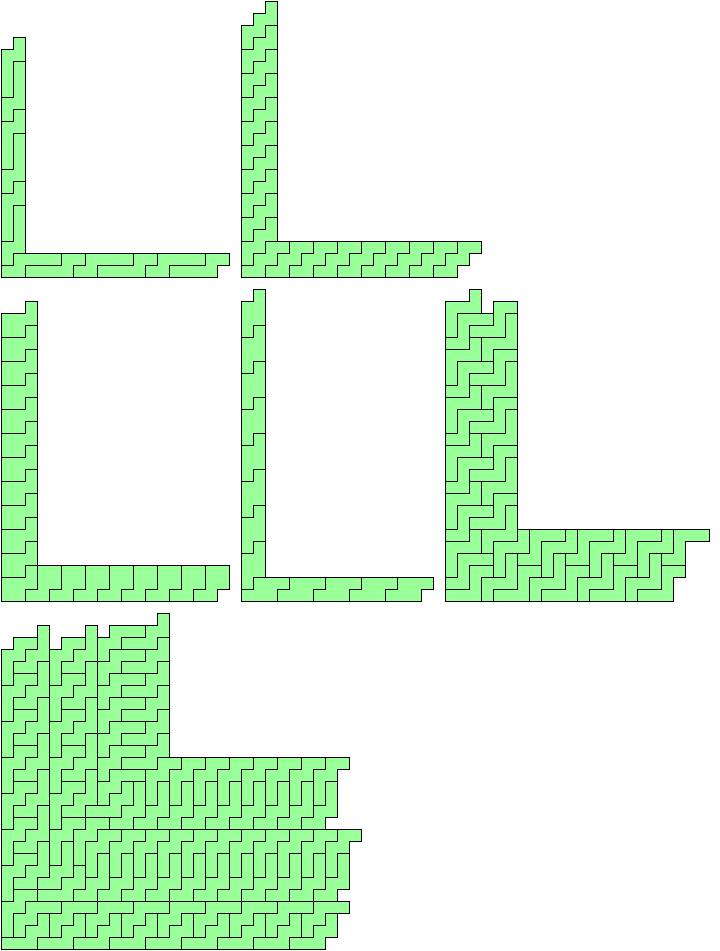
This is a strict hierarchy. Copies of a rectangle can form a bent strip. Two bent strips can form a branched strip, assuming that we do not require the arms to have equal width. Two branched strips can form crossed strips, again assuming that the arms' widths need not be equal.

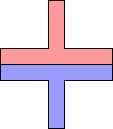
The tiling of an arm of a crossed strip must eventually repeat a configuration of tiles, so that a periodic tiling is possible, and so an infinite straight strip can be tiled. Infinite straight strips can tile the whole plane.

Other classes can be added to this classification, not necessarily preserving hierarchy. Golomb, in a 1966 paper, classified polyominoes with up to 6 cells by their ability to tile a rectangle, a bent strip, a half-infinite strip, an infinite strip, a quadrant, a half plane, and the plane.

It is not always easy to determine the class of a polyomino. Some of the classifications below are uncertain. If you find a higher-class tiling for a polyomino, please write!

For Class 1 tilings—rectifications—I show only the polyomino, not the tiling of the rectangle. You can find minimal known tilings at Mike Reid's Rectifiable Polyomino Page.

For Class 6 tilings—tilings of the whole plane—I show only the polyomino, not the tiling. For the tilings, see this page at Joseph Myers's site.

No polyominoes of order 6 or less belong to Class 7. All can tile the plane.