Pentomino Oddities
A polyomino oddity
is a symmetrical figure formed by an odd number of copies of
a polyomino.
Here are the minimal known oddities and extended oddities
for the 12 pentominoes,
as found mostly by
Mike Reid and me.
Click on the gray figures to expand them.
Holeless variants,
composite solutions,
and
nontrivial variants
are at the end of this page.
Figures with green backgrounds have holeless variants with
the same number of tiles.
Torsten Sillke was the first to investigate oddities.
For one-sided pentominoes, see
One-Sided Pentomino Oddities.
For hexominoes, see
Hexomino Oddities.
| Lateral | Diagonal | Rotary | Double
Lateral | Double
Diagonal | Double
Rotary | Full |
3
| 5
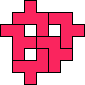
Mike Reid
| 7
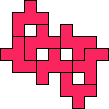
George Sicherman
| 9
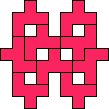
George Sicherman
| 15
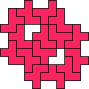
George Sicherman
| 17
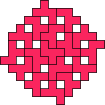
Mike Reid
| 21
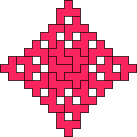
Mike Reid
|
1
| 5
| 1
| 1
| 5
| 5
| 5
|
7
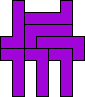
Mike Reid
| 5
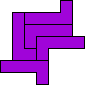
Mike Reid
| 7
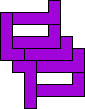
George Sicherman
| 11
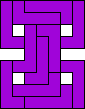
George Sicherman
| 13
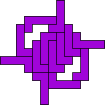
George Sicherman
| 13
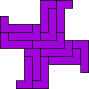
Mike Reid
| 21
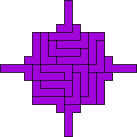
Mike Reid |
7
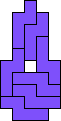
Mike Reid
| 5
Mike Reid
| 9
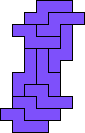
Mike Reid
| 15
George Sicherman
| 15
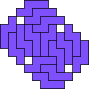
Mike Reid
| 21
George Sicherman
| 29
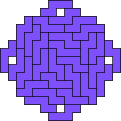
Mike Reid |
3
| 3
Torsten Sillke
| 5
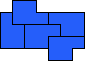
Torsten Sillke
| 9
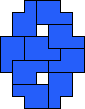
Mike Reid
| 7
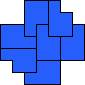
Torsten Sillke
| 9
Torsten Sillke
| 13
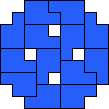
Mike Reid
|
1
| 17
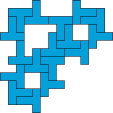
George Sicherman
| 23
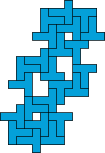
Mike Reid
| 31
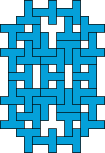
George
Sicherman
|
|
| |
1
| 13
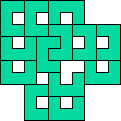
George Sicherman
| 19
George Sicherman
| 19
George Sicherman
|
|
|
|
11
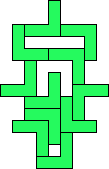
George Sicherman
| 1
| 15
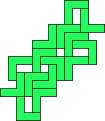
George Sicherman
|
| 33
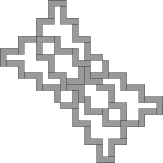
George
Sicherman
| 37
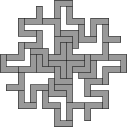
George
Sicherman
| |
7
George Sicherman
| 1
| 9
George Sicherman
| 21
Mike Reid
| 11
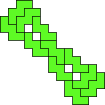
George Sicherman
| 25
George Sicherman
| 29
George Sicherman |
1
| 1
| 1
| 1
| 1
| 1
| 1
|
5
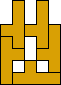
George Sicherman
| 7
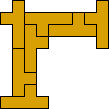
George Sicherman
| 7
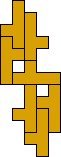
Mike Reid
| 13
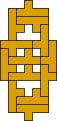
George Sicherman
| 17
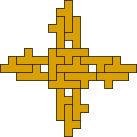
Mike Reid
| 17
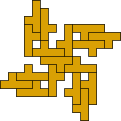
Mike Reid
| 29
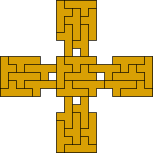
Mike Reid |
9
George Sicherman
| 13
George Sicherman
| 1
| 9
George Sicherman
| 13
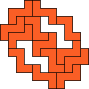
George Sicherman
| 13
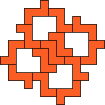
George Sicherman
| 73
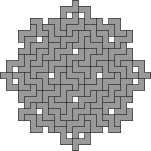
George
Sicherman
|
Lateral
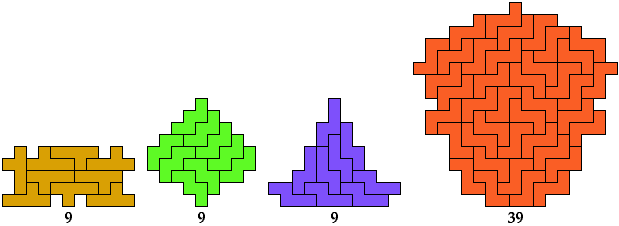
Diagonal
Birotary
Double Lateral
Double Diagonal
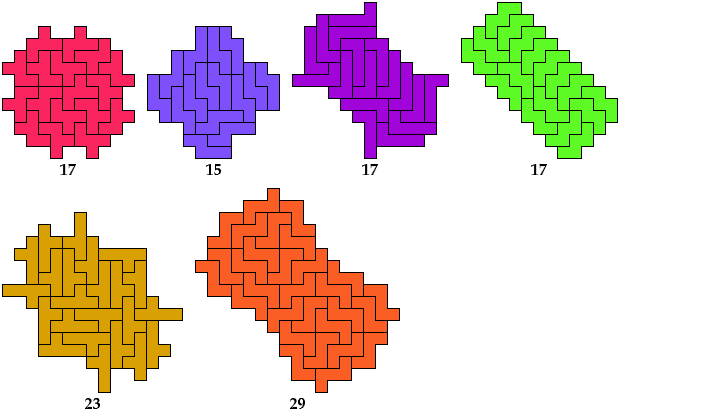
Double Rotary
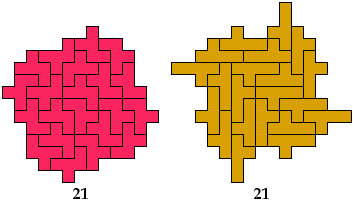
Full
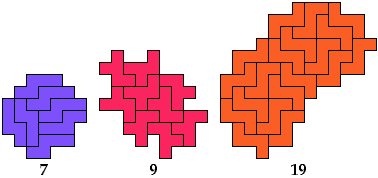
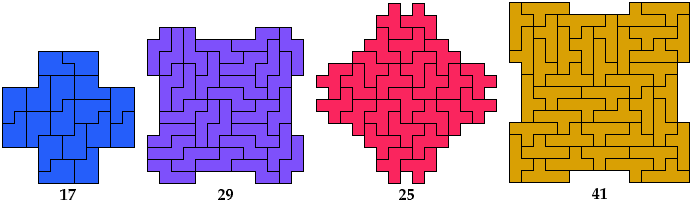Pentominoes T, U, and V have no known
oddities of some types.
However, they can form such oddities when combined in pairs.
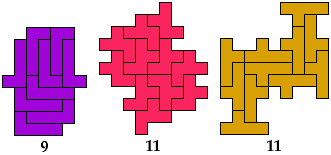
Double Diagonal
Double Rotary
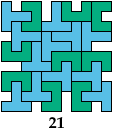
Full
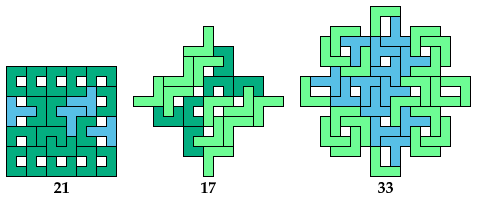These solutions have irreducible multiple tilings.
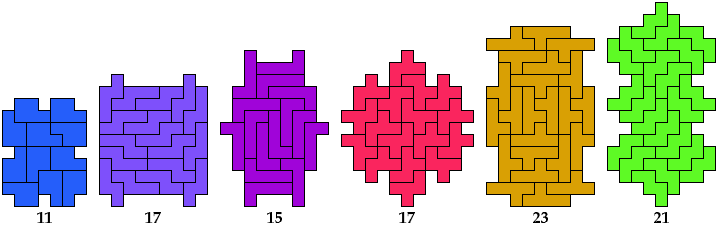
Lateral
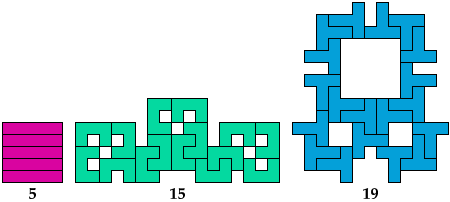
Diagonal
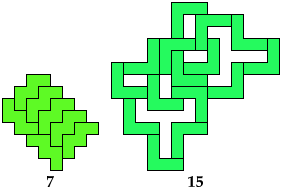
Rotary
Last revised 2023-02-16.
Back to Polyform Oddities
<
Polyform Curiosities
Col. George Sicherman
[ HOME
| MAIL
]
